Интеграл вдоль траекторий

Иллюстрация дерева путей, ведущих из точки A в точку B Интеграл вдоль траекторий – математический оператор, который используется в Фейнмановому формулировке квантовой механики.
Формальное определение интеграла вдоль траекторий дается формулой

,

где , – Множество всех траекторий, соединяющих начальную точку и конечную точку , M – масса квантовой частицы, – Сводная постоянная Планка.
Постулатом Фейманового формулировка квантовой механики является то, что пропагандиста задается интегралом вдоль траекторий:

,

где – Классическая действие.
В отличие от обычного интеграла, в котором суммируются значения функции на отрезке, в интеграле вдоль траекторий суммируются значения функции вдоль всех возможных кривых, соединяющих начальную и конечную точку. В рамках Фейнманового формулировка квантовой механики такой интеграл определяет амплитуду вероятности того, что квантовая частица переместится из начальной точки в конечную.
Если в классической механике реализуется и с траекторий, которой соответствует наименьшее значение действия, то в квантовой механике свой вклад в вероятность перехода частицы из одной точки в другую вносят все возможные кривые, соединяющие эти точки. Поскольку в квантовой механике определяется не вероятность перехода, а амплитуда вероятности, то взносы различных траекторий интерферируют.
Квантовую механику можно выразить через интегралы вдоль траекторий, используя также канонические переменные – координату и импульс. Пропагатора частицы задается при таком подходе через соотношение:

,

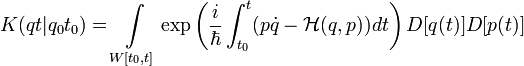где 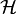– Функция Гамильтона.
Интегрирование проводится вдоль всех траекторий в фазовом пространстве с фиксированным значением координаты в начальной и конечной точках.
В квантовой статистической механике зележна от температуры матрица плотности удовлетворяет уравнению

,

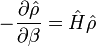где , K B – постоянная Больцмана.
Формальный решение этого уравнения

.

Статистическая сумма равна следа от матрицы плотности

.

Вводя условный «время» 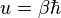, Где – Сводная постоянная Планка, и разбивая интервал [0, U] на мелкие интервалы, можно записать

,

рассматривая все возможные траектории, которыми система может переместиться из начального состояния при бесконечно высокой температуре в конечное состояние при температуре, определяется значением U.
Формулировка квантовой механики через интегралы вдоль траекторий разработал в 1948 году Ричард Фейнман.