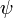Тождественные частиц
Тождественные частиц – одно из основных утверждений квантовой механики, согласно которому частицы одинакового рода никоим образом не возможно различить между собой и проиндексировать.
В отличие от классической физики, в квантовой механике положение частицы не является четко определенным в пространстве. Вероятность найти частицу в той или иной точке задается квадратом абсолютного значения волновой функции. Поэтому, каждая из одинаковых частиц имеет определенную вероятность находиться в какой-либо определенной точке пространства. При таких условиях невозможно различить, какую из них мы видим. Если в классической физике частицы одинаковы, мы все же можем мысленно присвоить каждой из них номер и отслеживать их траектории. В квантовой механике это невозможно.
Условие Тождественные частиц накладывает дополнительные требования к волнового функции многочастичного системы. Вероятность найти частицу в данной точке не зависит от произвольно присвоенного этой частице индекса. То есть, при изменении индексирования, вероятность должна остаться той же.
Взаимодействие между частицами зависит от расстояния между ними, а потому не меняется при перестановке частиц. Например, электрон, обозначенный индексом 1, взаимодействует с электроном, обозначенным индексом 2, внося вклад в потенциальной энергии квантомеханичнои системы . Если изменить нумерацию, и обозначить первый электрон индексом 2, а второй электрон индеском 1, то этот вклад в потенциальной энергии не изменится.
. Если изменить нумерацию, и обозначить первый электрон индексом 2, а второй электрон индеском 1, то этот вклад в потенциальной энергии не изменится.
Похоже утверждение справедливо относительно волновой функции. При перестановке частиц вероятность найти частицу данного сорта в любые точке пространства не должна измениться. Но волновая функция задает лишь амплитуду вероятности, поэтому при перестановке частиц волновая функция может остаться такой же, или же изменить знак на противоположный. Изменение знака волновой фунции не влияет на вероятность.
Таким образом, в квантовой механике существуют два вида частиц. Для одного из них при перестановке частиц знак волнового функции не меняется. Такие частицы называются бозонами.
Частицы, для которых волновая функция меняет знак при перестановке, называются фермионами.
Формально утверждение предыдущего параграфа приходится следующим образом.
Назовем оператором перестановок такое действие на любую многочастичных хвильвову функцию, переставляет индексы частиц.

Оператор перестановок коммутирует с гамильтонианом

Следовательно, оператор перестановок имеет общие с гамильтонианом собственные функции.
Пусть ? – собственная функция оператора перестановок с определенным собственным числом ?
 .
.
Очевидно, повторная действие оператора перестановок на функцию возвращает ее к первоначальному виду, а потому

Отсюда получаем уравнение для нахождения ?
? 2 = 1
Два возможных решения этого уравнения
? = 1 и
? = – 1,
а значит при перестановке часткок волновая функция или остается неизменной или меняет знак.
Нерозризнюванисть частиц в квантовой механике приводит к существованию особой квантовой статистики, различной для фермионов и бозонов. Фермионы подчиняются статистике Ферми-Дирака, бозоны – статистике Бозе-Эйнштейна.
Антисимметричность волновой функции электронов имеет следствием образования ковалентных связей (спаривание валентных электронов) в химических соединениях.
В отличие от классической физики, в квантовой механике положение частицы не является четко определенным в пространстве. Вероятность найти частицу в той или иной точке задается квадратом абсолютного значения волновой функции. Поэтому, каждая из одинаковых частиц имеет определенную вероятность находиться в какой-либо определенной точке пространства. При таких условиях невозможно различить, какую из них мы видим. Если в классической физике частицы одинаковы, мы все же можем мысленно присвоить каждой из них номер и отслеживать их траектории. В квантовой механике это невозможно.
Условие Тождественные частиц накладывает дополнительные требования к волнового функции многочастичного системы. Вероятность найти частицу в данной точке не зависит от произвольно присвоенного этой частице индекса. То есть, при изменении индексирования, вероятность должна остаться той же.
Взаимодействие между частицами зависит от расстояния между ними, а потому не меняется при перестановке частиц. Например, электрон, обозначенный индексом 1, взаимодействует с электроном, обозначенным индексом 2, внося вклад в потенциальной энергии квантомеханичнои системы
 . Если изменить нумерацию, и обозначить первый электрон индексом 2, а второй электрон индеском 1, то этот вклад в потенциальной энергии не изменится.
. Если изменить нумерацию, и обозначить первый электрон индексом 2, а второй электрон индеском 1, то этот вклад в потенциальной энергии не изменится.Похоже утверждение справедливо относительно волновой функции. При перестановке частиц вероятность найти частицу данного сорта в любые точке пространства не должна измениться. Но волновая функция задает лишь амплитуду вероятности, поэтому при перестановке частиц волновая функция может остаться такой же, или же изменить знак на противоположный. Изменение знака волновой фунции не влияет на вероятность.
Таким образом, в квантовой механике существуют два вида частиц. Для одного из них при перестановке частиц знак волнового функции не меняется. Такие частицы называются бозонами.
Частицы, для которых волновая функция меняет знак при перестановке, называются фермионами.
Формально утверждение предыдущего параграфа приходится следующим образом.
Назовем оператором перестановок такое действие на любую многочастичных хвильвову функцию, переставляет индексы частиц.

Оператор перестановок коммутирует с гамильтонианом

Следовательно, оператор перестановок имеет общие с гамильтонианом собственные функции.
Пусть ? – собственная функция оператора перестановок с определенным собственным числом ?
 .
.Очевидно, повторная действие оператора перестановок на функцию возвращает ее к первоначальному виду, а потому

Отсюда получаем уравнение для нахождения ?
? 2 = 1
Два возможных решения этого уравнения
? = 1 и
? = – 1,
а значит при перестановке часткок волновая функция или остается неизменной или меняет знак.
Нерозризнюванисть частиц в квантовой механике приводит к существованию особой квантовой статистики, различной для фермионов и бозонов. Фермионы подчиняются статистике Ферми-Дирака, бозоны – статистике Бозе-Эйнштейна.
Антисимметричность волновой функции электронов имеет следствием образования ковалентных связей (спаривание валентных электронов) в химических соединениях.
 Просмотров: 2544
Просмотров: 2544
 Дата: 16-02-2011
Дата: 16-02-2011
Локализованные состояния
Локализованыму состоянию квантовомеханической системы называется такое состояние, для которого вероятность пребывания за пределами определенной выбранной области очень быстро спадает по увеличению
ПОДРОБНЕЕ
Вектор состояния
Вектор состояния – совокупность характеристик, однозначно определяют состояние квантовой системы. Понятие вектор состояния является обобщением понятия волновой функции. Волновая функция, эволюция
ПОДРОБНЕЕ
Принцип запрета Паули
Принцип запрета Паули (или принцип запрета Паули) – квантово-механический принцип, согласно которому в многочастичных системе невзаимодействующих фермионов, никакие две частицы не могут описываться
ПОДРОБНЕЕ
Гамильтониан
Гамильтониан – оператор энергии в квантовой механике. Его спектр определяет все возможные значения энергии квантовой системы, которые можно получить при измерении. Название гамильтониан, как и
ПОДРОБНЕЕ
Квантовая запутанность
Квантовая запутанность – состояния квантовых систем, состоящих из множества частиц, в которых измерения определенной характеристики одной из частиц приводит к ограничению на значение этих свойств для
ПОДРОБНЕЕ
Волновая функция
Волновая функция, или пси-функция – Основной математический объект квантовой механики при ее формулировке, как волновой механики. В простейшем случае это комплексная квадратично интегрируема функция
ПОДРОБНЕЕ