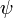Локализованные состояния
Локализованныму состоянию квантовомеханической системы называется такое состояние, для которого вероятность пребывания за пределами определенной выбранной области очень быстро спадает по увеличению расстояния до этой области.
В противном случае состояние называется делокализованым.
Локализованные состояния можно описать действительными волновыми функциями. Несмотря на это, эти состояния могут давать вклад в электрический ток.
Для локализованных состояний интеграл
 ,
,
в котором интегрирование проводится по координатном пространстве всех частиц, имеет конечное значение. Это обстоятельство позволяет нормировать волновую функцию таким образом, чтобы суммарная вероятность найти частицу во всем координатном пространстве равнялась бы единицы.
Атомы
Например, атом водорода состоит из протона и электрона. В атоме эти две частицы связаны между собой силами электростатического притяжения. Волновая функция электрона в основном состоянии спадает как , Где r – расстояние от протона, a 0 – радиус Бора. Вероятность того, что электрон будет находиться на расстоянии r от протона равен
, Где r – расстояние от протона, a 0 – радиус Бора. Вероятность того, что электрон будет находиться на расстоянии r от протона равен  и очень быстро уменьшается с увеличением расстояния.
и очень быстро уменьшается с увеличением расстояния.
Однако, возможны также случаи, когда электрон и протон находятся далеко друг от друга. При этом суммарная энергия частиц должна быть больше, чем энергия связи между ними. Для таких состояний вероятность найти электрон на любой расстоянии от протона практически не зависит от этой расстоянии. Такие состояния называются делокализованы.
Потенциальная яма
Локализованные и делокализованы состояния существуют также в случае модельной квантовомеханической задачи о доле в потенциальной яме, например, в полупроводниковой квантовой яме. Доля может локализоваться в яме в том случае, если яма достаточно глубока и широка.
Условие локализации можно оценить в Квазиклассическое приближение
 ,
,
где , E – энергия частицы, U (x) – потенциал, которым задается яма, m – масса частицы,
, E – энергия частицы, U (x) – потенциал, которым задается яма, m – масса частицы,  – Приведенная постоянная Планка, n – квантовое число, а интегрирование проводится по классически разрешенной области, где U (x)
– Приведенная постоянная Планка, n – квантовое число, а интегрирование проводится по классически разрешенной области, где U (x)
В противном случае состояние называется делокализованым.
Локализованные состояния можно описать действительными волновыми функциями. Несмотря на это, эти состояния могут давать вклад в электрический ток.
Для локализованных состояний интеграл
 ,
,в котором интегрирование проводится по координатном пространстве всех частиц, имеет конечное значение. Это обстоятельство позволяет нормировать волновую функцию таким образом, чтобы суммарная вероятность найти частицу во всем координатном пространстве равнялась бы единицы.
Атомы
Например, атом водорода состоит из протона и электрона. В атоме эти две частицы связаны между собой силами электростатического притяжения. Волновая функция электрона в основном состоянии спадает как
 , Где r – расстояние от протона, a 0 – радиус Бора. Вероятность того, что электрон будет находиться на расстоянии r от протона равен
, Где r – расстояние от протона, a 0 – радиус Бора. Вероятность того, что электрон будет находиться на расстоянии r от протона равен  и очень быстро уменьшается с увеличением расстояния.
и очень быстро уменьшается с увеличением расстояния.Однако, возможны также случаи, когда электрон и протон находятся далеко друг от друга. При этом суммарная энергия частиц должна быть больше, чем энергия связи между ними. Для таких состояний вероятность найти электрон на любой расстоянии от протона практически не зависит от этой расстоянии. Такие состояния называются делокализованы.
Потенциальная яма
Локализованные и делокализованы состояния существуют также в случае модельной квантовомеханической задачи о доле в потенциальной яме, например, в полупроводниковой квантовой яме. Доля может локализоваться в яме в том случае, если яма достаточно глубока и широка.
Условие локализации можно оценить в Квазиклассическое приближение
 ,
,где
 , E – энергия частицы, U (x) – потенциал, которым задается яма, m – масса частицы,
, E – энергия частицы, U (x) – потенциал, которым задается яма, m – масса частицы,  – Приведенная постоянная Планка, n – квантовое число, а интегрирование проводится по классически разрешенной области, где U (x)
– Приведенная постоянная Планка, n – квантовое число, а интегрирование проводится по классически разрешенной области, где U (x)
 Просмотров: 3289
Просмотров: 3289
 Дата: 24-02-2011
Дата: 24-02-2011
Основное состояние квантовомеханической системы
Основным состоянием квантовомеханической системы называется стационарное состояние с наименьшей энергией. В квантовой механике спектр гамильтониана, т.е. спектр возможных значений энергии, всегда
ПОДРОБНЕЕ
Вектор состояния
Вектор состояния – совокупность характеристик, однозначно определяют состояние квантовой системы. Понятие вектор состояния является обобщением понятия волновой функции. Волновая функция, эволюция
ПОДРОБНЕЕ
Принцип запрета Паули
Принцип запрета Паули (или принцип запрета Паули) – квантово-механический принцип, согласно которому в многочастичных системе невзаимодействующих фермионов, никакие две частицы не могут описываться
ПОДРОБНЕЕ
Гамильтониан
Гамильтониан – оператор энергии в квантовой механике. Его спектр определяет все возможные значения энергии квантовой системы, которые можно получить при измерении. Название гамильтониан, как и
ПОДРОБНЕЕ
Тождественные частиц
Тождественные частиц – одно из основных утверждений квантовой механики, согласно которому частицы одинакового рода никоим образом не возможно различить между собой и проиндексировать. В отличие от
ПОДРОБНЕЕ
Волновая функция
Волновая функция, или пси-функция – Основной математический объект квантовой механики при ее формулировке, как волновой механики. В простейшем случае это комплексная квадратично интегрируема функция
ПОДРОБНЕЕ