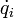Гармонический осциллятор

Колебания гармонического осциллятора Гармоничным осциллятором называется физический объект, эволюция которого со временем описывается дифференциальным уравнением

,

где q – обобщенная координата гармонического осциллятора, t – время, ? – характерная частота гармонического осциллятора. Две точки над переменной означают вторую производную по времени. Величина q совершающий гармонические колебания.
Задача о гармоничном осциллятор играет центральную роль как в классической, так и в квантовой физике.
Большое количество физических систем ведут себя как гармоничные осциллятора при малом отклонении от равновесия. К ним относятся математический и физический маятники, колебания атомов в молекулах и твердых телах, электрические колебательные контуры и многие другие.
Малые колебания маятника являются гармоническими

Энергия, функция Лагранжа и Гамильтона
Кинетическая энергия гармонического осциллятора задается выражением

.

Потенциальная энергия гармонического осциллятора задается выражением

.

Соответственно, считая величину q обобщенной координатой, функция Лагранжа гармоничного осцлятора записывается

.

Обобщенный импульс



Функция Гамильтона

.

Вынужденные колебания
Под действием внешней периодической силы с частотой, которая не обязательно совпадает с собственной частотой гармонического осциллятора, осциллятор совершает гармонические колебания, аплитуда которых определяется величиной внешней силы и соотношением внешней частоты и собственной частоты осциллятора.
Вынужденные колебания гармонического осциллятора с частотой ? 0 под действием силы с частотой ?описуються уравнением

,

где f 0 – амплитуда внешней силы.
Частное решение этого уравнения, описывающий вынужденные колебания имеет вид

.

Гармоничный осцитор под действием внешней силы совершающий гармонические колебания с амплитудой . При амплитуда вынужденных колебаний стремится к бесконечности. Это явление называется резонансом.
Гармонический осциллятор с затуханием
При учете сил трения или сопротивления другого рода, который приводит к диссипации энергии осциллятора и превращении ее в тепло, уравнение гармонического осциллятора меняются. В частности очень распространенный случай, когда силы сопротивления пропорциональны скорости изменения величины q. Тогда уравнение гармонического осциллятора принимает вид

.

Такие колебания затухают со временем по закону

.

Вынужденные колебания гармонического осциллятора с затуханием
При действии периодической внешней силы даже при затухании для осциллятора устанавливаются гармонические колебания с амплитудой, зависящей от приложенной силы, соотношение частот, а также от величины затухания.
Амплитуда вынужденных колебаний с учетом затухания определяется формулой

.

Это конечная величина при всех частотах внешней силы.
Математический маятник при небольшом начальном отклонении от вертикали совершающий гармонические колебания с частотой



Колебательный контур гармоническим осциллятором, с частотой

,

где L – индуктивность, C – емкость.
Подробнее см. Квантовый осциллятор.
Спектр собственных значений и собственных функциях
Волновые функции первых шести состояний с квантовыми числами от n = 0 до 5. На оси ординат отложена обобщенная координата Гамильтониан гармонического осциллятора получается заменой в функции Гамильтона импульса p на

.

Спектр гармонического осциллятора находится со стационарного уравнения Шредингера и задается формулой

.

Здесь n – квантовое число, пробегает значения от нуля до бесконечности. Энергетические уровни гармонического осциллятора эквидистантных. Характерной особенностью гармонического осциллятора является то, что даже в основном состоянии гармоничный осциллятор имеет отличную от нуля энергию

.

Эта низкая энергия называется энергией нулевых колебаний.
Собственные функции гармонического осциллятора, соответствующих квантовому числу n задаются формулами

,

где , А H n (x) – полиномы Эрмита.
При четном n собственные функции гармонического осциллятора парные, при Непрану – нечетные. Гамильтониан гармонического осциллятора коммутирует с оператором замены x на – x (оператором четности), а потому имеет общие собственные функции с этим оператором.
Операторы рождения и уничтожения
Если определить оператор рождения



и оператор уничтожения

,

то

.

Операторы рождения и уничтожения удовлетворяют коммутационном соотношению:

.

Собственные функции гармонического осциллятора тогда имеют вид

,

или, используя нотацию кет и бра-векторов:

.

Всего действие оператора рождения на гармоничное оператор в состоянии | n> приводит к переходу в состояние | n +1>:

.

Действие оператора уничтожения на состояние | n> приводит к переходу в состояние | n-1>:



Оператор



называют оператором числа частиц, поскольку для него справедливо соотношение.



Правила отбора
При излучении или поглощении фотона разрешенными переходами для гармонического осциллятора есть такие, при которых квантовое число n изменяется на единицу. Учитывая еквидистантнисть уровней, это правило отбора приводит к тому, что, несмотря на бесконечное число уровней, в спектре оптического поглощения или излучения гармонического осциллятора есть только одна линия с частотой ?.
В реальных колебательных спектрах молекул возможны отклонения от этого правила, обусловленные ангармоничнистю реального потенциала межатомного взаимодействия, квадрупольными переходами и т.д.