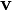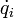Механика Гамильтона
Гамильтонова механика это одна из формулировок законов механики, в общем аналогичное законам Ньютона, но удобное для обобщений, использование в статистической физике и для перехода к квантовой механике.
Функция Гамильтона определяется через обобщенные координаты
определяется через обобщенные координаты  и обобщенные импульсы
и обобщенные импульсы  исходя из функции Лагранжа
исходя из функции Лагранжа  следующим образом.
следующим образом.
Обобщенные импульсы определяются, как
 .
.
Функция Гамильтона определяется согласно
 .
.
После этого все обобщенные скорости d
d  выражаются через обобщенные импульсы и координаты.
выражаются через обобщенные импульсы и координаты.
По своей сути функция Гамильтона является энергией системы, выраженной через координаты и импульсы.
В случае стационарных связей и потенциальных внешних сил
 ,
,
т.е. функция Гамильтона является суммой потенциальной и кинетической энергий, но при этом кинетическая энергия должна быть выражена через импульсы, а не через скорости.
Уравнения эволюции динамической системы записываются в гамильтоновой механике в виде
 ,
,
 .
.
Эти уравнения называются каноническими уравнениями Гамильтона. Они полностью определяют эволюцию системы с течением времени в том смысле, что зная значение обобщенных координат и скоростей в определенный начальный момент времени, можно определить их значение в любой последующий момент времени, решая данную систему уравнений.
Функция Гамильтона для заряда в электромагнитном поле
Всего сила Лоренца не является потенциальной силой, поскольку зависит от скорости движения заряда. Однако ее можно включить в Гамильтоновы механику записав функцию Гамильтона заряженной частицы в следующей форме:

где e – заряд частицы, – Электростатический потенциал,
– Электростатический потенциал,  – Векторный потенциал.
– Векторный потенциал.
В релятивистском случае будем иметь:
 .
.
Функция Гамильтона в теории относительности
Функцию Гамильтона в релятивистском случае можно получить путем стандартной процедуры, зная функцию Лагранжа (См. "Механику" Ландау):
(См. "Механику" Ландау):

Как видно, ее выражение полностью совпадает с выражением для потенциальной энергии релятивистской частицы, и не зависит в явной форме от импульса. Зная релятивистский импульс, это выражение можно переписать в виде квадратичной формы:
 ,
,
из которой и получаем общепризнанный выражение для функции Гамильтона:
 .
.
Это выражение для функции Гамильтона широко используется в классической и квантовой механике.
Использование в квантовой механике
В квантовой механике оператор энергии строится по классической функции Гамильтона заменой обобщенных импульсов p i на операторы импульса
строится по классической функции Гамильтона заменой обобщенных импульсов p i на операторы импульса  , Где
, Где  – Сводная постоянная Планка. Такой оператор называется гамильтонианом, а процедура перехода от функции Гамильтона к гамильтониану называется процедурой квантования.
– Сводная постоянная Планка. Такой оператор называется гамильтонианом, а процедура перехода от функции Гамильтона к гамильтониану называется процедурой квантования.
Гамильтониан является главным оператором в квантовой механике, поскольку входит в главное уравнения квантовой механики – уравнение Шредингера.
Механический осциллятор
В случае классического механического осциллятора (без трения) функция Гамильтона имеет следующий вид:

где k – коэффициент упругости, а m – масса частицы.
Первое дифференциальное уравнение, равное
 ,
,
из которого получаем выражение для импульса:
 .
.
Второе дифференциальное уравнение Гамильтона имеет вид:
 ,
,
откуда уравнение движения:

или в стандартной форме:
 .
.
Можно также привести значение "действия" на промежутке одного периода колебаний:

где a – амплитуда колебаний, циклическая частота, а T = 2? / ? – период.
циклическая частота, а T = 2? / ? – период.
Электрический осциллятор
Для классического L C – контура функция Гамильтона имеет вид:

где "Магнитный импульс" (фактически – магнитный поток).
"Магнитный импульс" (фактически – магнитный поток).
Можно также привести значение "действия" на промежутке одного периода колебаний:

где q 0 – амплитудное значение заряда, период колебаний.
период колебаний.
Механика Лагранжа
Уравнение Гамильтона-Якоби
скобки Пуассона
Функция Гамильтона
 определяется через обобщенные координаты
определяется через обобщенные координаты  и обобщенные импульсы
и обобщенные импульсы  исходя из функции Лагранжа
исходя из функции Лагранжа  следующим образом.
следующим образом.Обобщенные импульсы определяются, как
 .
.Функция Гамильтона определяется согласно
 .
.После этого все обобщенные скорости
 d
d  выражаются через обобщенные импульсы и координаты.
выражаются через обобщенные импульсы и координаты.По своей сути функция Гамильтона является энергией системы, выраженной через координаты и импульсы.
В случае стационарных связей и потенциальных внешних сил
 ,
,т.е. функция Гамильтона является суммой потенциальной и кинетической энергий, но при этом кинетическая энергия должна быть выражена через импульсы, а не через скорости.
Уравнения эволюции динамической системы записываются в гамильтоновой механике в виде
 ,
, .
.Эти уравнения называются каноническими уравнениями Гамильтона. Они полностью определяют эволюцию системы с течением времени в том смысле, что зная значение обобщенных координат и скоростей в определенный начальный момент времени, можно определить их значение в любой последующий момент времени, решая данную систему уравнений.
Функция Гамильтона для заряда в электромагнитном поле
Всего сила Лоренца не является потенциальной силой, поскольку зависит от скорости движения заряда. Однако ее можно включить в Гамильтоновы механику записав функцию Гамильтона заряженной частицы в следующей форме:

где e – заряд частицы,
 – Электростатический потенциал,
– Электростатический потенциал,  – Векторный потенциал.
– Векторный потенциал.В релятивистском случае будем иметь:
 .
.Функция Гамильтона в теории относительности
Функцию Гамильтона в релятивистском случае можно получить путем стандартной процедуры, зная функцию Лагранжа
 (См. "Механику" Ландау):
(См. "Механику" Ландау):
Как видно, ее выражение полностью совпадает с выражением для потенциальной энергии релятивистской частицы, и не зависит в явной форме от импульса. Зная релятивистский импульс, это выражение можно переписать в виде квадратичной формы:
 ,
,из которой и получаем общепризнанный выражение для функции Гамильтона:
 .
.Это выражение для функции Гамильтона широко используется в классической и квантовой механике.
Использование в квантовой механике
В квантовой механике оператор энергии
 строится по классической функции Гамильтона заменой обобщенных импульсов p i на операторы импульса
строится по классической функции Гамильтона заменой обобщенных импульсов p i на операторы импульса  , Где
, Где  – Сводная постоянная Планка. Такой оператор называется гамильтонианом, а процедура перехода от функции Гамильтона к гамильтониану называется процедурой квантования.
– Сводная постоянная Планка. Такой оператор называется гамильтонианом, а процедура перехода от функции Гамильтона к гамильтониану называется процедурой квантования.Гамильтониан является главным оператором в квантовой механике, поскольку входит в главное уравнения квантовой механики – уравнение Шредингера.
Механический осциллятор
В случае классического механического осциллятора (без трения) функция Гамильтона имеет следующий вид:

где k – коэффициент упругости, а m – масса частицы.
Первое дифференциальное уравнение, равное
 ,
,из которого получаем выражение для импульса:
 .
.Второе дифференциальное уравнение Гамильтона имеет вид:
 ,
,откуда уравнение движения:

или в стандартной форме:
 .
.Можно также привести значение "действия" на промежутке одного периода колебаний:

где a – амплитуда колебаний,
 циклическая частота, а T = 2? / ? – период.
циклическая частота, а T = 2? / ? – период.Электрический осциллятор
Для классического L C – контура функция Гамильтона имеет вид:

где
 "Магнитный импульс" (фактически – магнитный поток).
"Магнитный импульс" (фактически – магнитный поток).Можно также привести значение "действия" на промежутке одного периода колебаний:

где q 0 – амплитудное значение заряда,
 период колебаний.
период колебаний.Механика Лагранжа
Уравнение Гамильтона-Якоби
скобки Пуассона
 Просмотров: 3978
Просмотров: 3978
 Дата: 16-02-2011
Дата: 16-02-2011
Кинетическая энергия
Кинетическая энергия – часть энергии физической системы, которую она имеет благодаря движения. Кинетическую энергию принято обозначать буквами K или T. В случае частицы с массой m и скоростью
ПОДРОБНЕЕ
Закон сохранения энергии
Закон сохранения энергии (рус. закон сохранения энергии; англ. Energy conservation law; нем. Erhaltungssatz n der Energie f, Energieerhaltungsgesetz n, Gesetz n der Erhaltung f der Energie f) –
ПОДРОБНЕЕ
Механика Лагранжа
Механика Лагранжа – один из возможных формулировок классической механики, аналогичное по своей сути законам Ньютона. В физике механика в формулировке Лагранжа оперирует с обобщенными координатами и
ПОДРОБНЕЕ
Статистическая механика
Статистическая механика – раздел физики, который, используя статистический подход теории вероятности, изучает макроскопические свойства физических систем, состоящих из большого числа частиц. Несмотря
ПОДРОБНЕЕ
Интеграл вдоль траекторий
Иллюстрация дерева путей, ведущих из точки A в точку B Интеграл вдоль траекторий – математический оператор, который используется в Фейнмановому формулировке квантовой механики. Формальное определение
ПОДРОБНЕЕ
Гамильтониан
Гамильтониан – оператор энергии в квантовой механике. Его спектр определяет все возможные значения энергии квантовой системы, которые можно получить при измерении. Название гамильтониан, как и
ПОДРОБНЕЕ