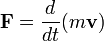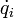Классическая механика

Классическая механика – это раздел физики, изучающий движение на основе законов Ньютона. Классическая механика подразделяется на:
Базовыми понятиями классической механики является понятие силы, массы и движения. Масса в классической механике определяется как мера инерции, или способности тела к сохранению состояния покоя или равномерного прямолинейного движения при отсутствии воздействия на него сил. С другой стороны, силы, действующие на тело, изменяют состояние его движения, вызывая ускорение. Взаимодействие этих двух эффектов и является главной темой механики Ньютона.
Другими важными понятиями этого раздела физики есть энергия, импульс, момент импульса, которые могут передаваться между объектами в процессе взаимодействия. Энергия механической системы складывается из ее кинетической (энергии движения) и потенциальной (зависимой от положения тела относительно других тел) энергий. Относительно этих физических величин действуют фундаментальные законы сохранения.
Основы классической механики были заложены Галилеем, а также Коперником и Кеплером при изучении закономерностей движения небесных тел, и долгое время механика и физика рассматривались в контексте  астрономических событий.
В своих работах Коперник отмечал, что вычисление закономерностей движения небесных тел может быть значительно упрощен, если отойти от принципов, заложенных Аристотелем, и считать Солнце, а не Землю, отправной точкой для таких вычислений, т.е. осуществить переход от геоцентрической к гелиоцентрической систем.
Идеи гелиоцентрической системы дальше были формализованы Кеплером в его трех законах движения небесных тел. В частности, из второго закона следовало, что все планеты солнечной системы движутся эллиптическими орбитами, имеющие одним из своих фокусов Солнце.
Следующий важный вклад в основание классической механики был осуществлен Галилеем, который, исследуя фундаментальные закономерности механического движения тел, в частности под воздействием сил земного притяжения, сформулировал пять универсальных законов движения.
Но все же лавры основного основателя классической механике относятся Исааку Ньютону, который в своей работе «Математические начала натуральной философии» осуществил синтез тех понятий по физике механического движения, которые были сформулированы его предшественниками. Ньютон сформулировал три фундаментальные законы движения, которые были названы его именем, а также закон всемирного тяготения, который подводил черту под исследованиями Галилеем феномена свободного падения тел. Таким образом, была создана новая, на замену устаревшей Аристотелевой, картина мира базовых его законов.
Классическая механика дает точные результаты для систем, которые мы встречаем в повседневной жизни. Но они становятся некорректными для систем, скорость которых приближается к скорости света, где она заменяется релятивистской механикой, либо для очень малых систем, где действуют законы квантовой механики. Для систем, которые объединяют оба эти свойства, вместо классической механики обеими характеристиками – квантовая теория поля. Для систем с очень большим количеством составляющих, или степеней свободы, классическая механика также быть адекватной, зато используются методы статистической механики
Классическая механика сохраняет, потому что она, во-первых, гораздо проще в применении, чем остальные теории, и, во-вторых, имеет большие возможности для аппроксимации и применение для очень широкого класса физических объектов, начиная со привычных, таких как волчок или мяч, многих астрономических объектов (планеты, галактики) и совсем микроскопических).
Хотя классическая механика в общих чертах совместима с другими «классическими теориями, такими как классическая электродинамика и термодинамика, имеются некоторые несоответствия между этими теориями, которые были найдены в конце 19 века. Они могут быть решены методами более современной физики. В частности, классическая электродинамика предсказывает, что скорость света постоянна, что несовместимо с классической механикой и привело к созданию специальной теории относительности. Принципы классической механики рассмотрении совместно с утверждениями классической термодинамики, что приводит к парадоксу Гиббса, согласно которому невозможно точно определить величину энтропии и к ультрафиолетовой катастрофе, в которой абсолютно черное тело должно излучать бесконечное количество энергии. Для преодоления этих несоответствий была создана квантовая механика.
Объекты, которые изучаются механикой, называются механическими системами. Задачей механики является изучение свойств механических систем, в частности их эволюции во времени.
Базовый математический аппарат классической механики – дифференциальное и интегральное исчисление, разработанное специально для этого Ньютоном и Лейбницем. В классическом формулировке механика строится на трех законах Ньютона.
Далее дается изложение базовых концепций классической механики. Для простоты будем рассматривать только материальную точку объекта, размерами которого можно пренебречь. Движение материальной точки характеризуется несколькими параметрами: ее положением, массой, и приложенными к ней силами.
В реальности, размеры каждого объекта, с которым имеет дело классическая механика, является ненулевыми. Материальные точки, такие, как электрон, подчиняются законам квантовой механики. Объекты ненулевого размера могут испытывать более сложные движения, поскольку их внутреннее состояние может меняться – например, мяч может еще и вращаться. Тем не менее, к таким телам результаты, полученные для материальных точек, рассматривая их как совокупности большого количества взаимодействующих материальных точек. Такие сложные тела ведут себя как материальные точки, если их малы в масштабах рассматриваемой задачи.
Радиус-вектор и его производные
Положение объекта материальной точки определяется относительно фиксированной точки в пространстве, которая называется началом координат. Оно может быть задано координатами этой точки (например, в прямоугольной системе координат) или радиус-вектором r, проведенным из начала координат в эту точку. В реальности, материальная точка может двигаться с течением времени, поэтому радиус-вектор в общем случае является функцией времени. В классической механике, в отличие от релятивистской, считается, что течение времени является одинаковым во всех системах отсчета.
Траектория
Траекторией называется совокупность всех положений материальной точки, движущейся – в общем случае она является кривой линией, вид которой зависит от характера движения точки и выбранной системы отсчета.
Перемещение
Перемещение – это вектор, соединяющий начальное и конечное положение материальной точки.
Скорость
Скорость, или отношение перемещения ко времени, в течение которого оно происходит, определяется как первая производная от перемещения к времени:

.

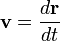В классической механике, скорости можно добавлять и отнимать. Например, если одна машина едет на запад со скоростью 60 км / ч, и догоняет другую, которая движется в том же направлении со скоростью 50 км / ч, то относительно второй машина первая движется на запад со скоростью 60-50 = 10 км / ч. Зато на перспективу быстрые машины, медленнее движется со скоростью 10 км / ч на восток.
Для определения относительной скорости в любом случае применяются правила векторной алгебры для составления векторов скорости.
Ускорение
Ускорение, или скорость изменения скорости – это производная от скорости до времени или вторая производная от перемещения к времени:

.

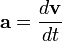Вектор ускорения может меняться по величине, так и по направлению. В частности, если скорость уменьшается, иногда ускорение "замедлением, но вообще любую изменению скорости.
Силы. Второй закон Ньютона
Второй закон Ньютона утверждает, что ускорение материальной точки является прямо пропорциональным силе, на нее действует, а вектор ускорения направлен по линии действия этой силы. Иными словами, этот закон связывает силу, которая действует на тело с его массой и ускорением. Тогда второй закон Ньютона выглядит так:

.

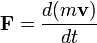Величина m v называется импульсом. Обычно, масса m не изменяется со временем, и закон Ньютона можно записать в упрощенной форме



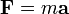
где а – ускорение, которое было определено выше. Масса тела m Не всегда с течением времени. Например, масса ракеты уменьшается по мере использования горючего. При таких обстоятельствах, последнее выражение неприменимо, и следует пользоваться полной формой второго закона Ньютона.
Второго закона Ньютона недостаточно для описания движения частицы. Он требует определения той силы, которая на нее действует. Например, типичный выражение для силы трения при движении тела в газе или в жидкости определяется следующим образом:



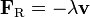
где ? – некоторая константа, которая называется коэффициентом трения.
После того как определены все силы, на базе второго закона Ньютона получим дифференциальное уравнение, называемое уравнением движения. В нашем примере с лишь одной силой, которая действует на частицу, получим:

.

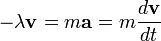Проинтегрировав, получим:



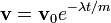
где 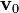– Начальная скорость. Это означает, что скорость движения нашего объекта уменьшается экспоненциально до нуля. Это выражение в свою очередь может быть вновь проинтегровано для получения выражения для радиус-вектора r тела в зависимости от времени.
Если на частицу действуют несколько сил, то они добавляются по правилам сложения векторов.
Энергия
Если сила F действует на частицу, которая в результате этого перемещается на ? r, то при этом выполняется работа, равный:

.

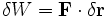Если масса частицы стала, то тоскуя работы, выполненные всеми силами, из второго закона Ньютона

,

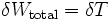Где Т – кинетическая энергия. Для материальной точки определяется как

.

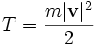Для сложных объектов из множества частиц, кинетическая энергия тела равна сумме кинетических энергий всех частиц.
Особый класс консервативных сил может быть выражен градиентом скалярной функции, известной как потенциальная энергия V:



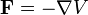
Если все силы, действующие на частицу консервативны, а V – полная потенциальная энергия, полученная добавлением потенциальных энергий всех сил, то
Т.е. полная энергия E = T + V сохраняется во времени. Это проявление одного из фундаментальных физических законов сохранения. В классической механике он может быть полезным практически, ведь много разновидностей сил в природе являются консервативными.
Законы Ньютона имеют несколько важных последствий для твердых тел (см. момент импульса)
Существуют также два важных альтернативные формулировки классической механики: механика Лагранжа и гамильтонова механика. Они эквивалентны механике Ньютона, но иногда оказываются полезными для анализа некоторых проблем. Они, как и другие современные формулировки, не используют понятие силы, вместо обращаясь к другим физических величин, таких как энергия.