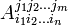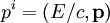Тензор энергии-импульса
Тензор энергии-импульса – симметричный 4-тензор, определенный в пространстве-времени, который одновременно задает плотность энергии и ее потоков и определяет закон изменения этих величин при переходе от одной системы отсчета к другой.
Тензор энергии-импульса в общем случае имеет вид:

где W – плотность энергии, S i – поток энергии в направлении, задаваемом координатой i, , Где ? i j – тензор в обычном пространстве, которое называют тензором напряжений.
, Где ? i j – тензор в обычном пространстве, которое называют тензором напряжений.
Для тензора энергии-импульса справедливо соотношение
 ,
,
которое является локальным выражением законов сохранения энергии и импульса.
Очевидна также симметрия тензора энергии-импульса T i j относительно перестановок индексов. Это свойство выражает локальный закон сохранения момента импульса.
Значение тензора энергии-импульса в том, что он входит в основной уравнения общей теории относительности – уравнение Эйнштейна, и, таким образом позволяет дополнить эти уравнения ривннямы состояния вещества.
В классической механике движение непрерывного вещества описывает гидродинамика и теория упругости твердых тел. Каждая частица вещества в точке 3-мерного пространства (x, y, z) и в некоторый момент времени t описывается плотностью:

а также скоростью в этой точке:

и тензором напряжений ? ??, описывающий силовое взаимодействие частицы вещества с соседними частицами.

В случае жидкости или газа, тензор напряжений диагональный и выражается через давление p формуле:

Поскольку вещество "размазана" в пространстве, выделим в какой момент времени (t = t 0) элемент объема ? V. Размер четыре-вектора энергии-импульса ? p ? для части вещества, попавшего в этот объем, пропорциональна самому объема с некоторыми коэффициентами пропорциональности :
:

Левая часть этого уравнения есть четыре-вектором. Исследуем, с точки зрения тензорного анализа, что собой представляет произведение в правой части уравнения.
Начнем с трехмерного объема ? V, представив его в виде параллелепипеда, построенного на трех векторах . Эти векторы можно считать четыре-векторами, с нулевой первой (временной) координате. Объем является величиной тензора третьего ранга, составленный внешним произведением этих векторов:
. Эти векторы можно считать четыре-векторами, с нулевой первой (временной) координате. Объем является величиной тензора третьего ранга, составленный внешним произведением этих векторов:

Пользуясь единичным антисимметричным тензором, мы можем также составить дуальный четыре-вектор:

где g – детерминант метрического тензора.
В этой формуле множитель мнимой единицы введено для того, чтобы компоненты вектора ? V ? были действительными числами. Величина этого вектора равна объему ? V, а направление ортогональный к составляющим векторов . То есть в выбранной системе координат он направлен вдоль оси времени:
. То есть в выбранной системе координат он направлен вдоль оси времени:

Теперь мы можем, меняя при необходимости обозначения коэффициентов переписать формулу (7) так:
переписать формулу (7) так:

В этой формуле мы сначала вели еще один индекс "ноль" в обозначении коэффициентов, а потом чисто формально добавили еще три нулевые слагаемые (поскольку согласно (10) пространственные компоненты вектора ? V равны нулю).
Правая часть формулы (11) имеет вид произведению скорости света на свертке тензора второго ранга с вектором. Обозначим тензор и назовем его тензором энергии-импульса. Тогда четыре-вектор энергии-импульса вещества, попавшего в элемент объема ? V, согласно формуле (11) запишется в виде свертки тензора энергии-импульса с чотиривектором объема:
и назовем его тензором энергии-импульса. Тогда четыре-вектор энергии-импульса вещества, попавшего в элемент объема ? V, согласно формуле (11) запишется в виде свертки тензора энергии-импульса с чотиривектором объема:

Расписывая покомпонентно формулу (12) и учитывая (6) находим, что если ? = 0


то есть верхний левый элемент матрицы T имеет смысл плотности энергии.
Теперь приравняем индекс ? одной из пространственных координат, например ? = 1. Тогда

Откуда мы можем выразить T 10 двумя способами, учитывая связь импульса с массой ? p 1 = ? m v 1 и формулу Эйнштейна ? E = ? m c 2:

Соответственно имеем две трактовки компоненты T 10: или плотность проекции импульса, умноженная на скорость света, или поток энергии в направлении оси абсцисс, разделенный на скорость света.
В классической механике совокупный импульс системы физических тел и электромагнитного поля сохраняется, т.е. не изменяется со временем. То же касается энергии, если розглядиты действие только консервативных сил. Попробуем выяснить, как эти законы сохранения отражаются в теории относительности на свойствах тензора энергии-импульса.
Начнем с того, что энергия и импульс образуют четыре-вектор (6). Операцию сложения двух пространственно-разнесенных векторов можно осуществить, совершив параллельное перенесение одного вектора в точку нахождения другого. Такая операция будет однозначным только для плоского пространства, с нулевым тензором Римана. Итак начнем с рассмотрения небольшой, ограниченной в пространстве механической системы, гравитационным полем которой (а следовательно и искривлением пространства) можно пренебречь. Для этого надо, чтобы все массы тел были достаточно малыми. Систему координат будем считать прямоугольная декартова.
Выберем фиксированный момент времени t = t (1) i найдем общий четыре-вектор энергии-импульса системы, интегрировать формулу (12) по всему трехмерному пространству (который является гиперплоскостью в четырехмерном пространстве-времени):

В другой момент времени t = t (2) четыре-вектор энергии-импульса останется неизменным, и нулевую разницу мы можем записать в виде интеграла по четырехмерном прослойки между двумя гиперплоскостями:

В последнем интеграле дифференциал d ? является инвариантным элементом четырехмерного объема (см. Интегрирование по объему многообразиях):

Поскольку все физические законы должны носить тензорный характер (а значит не зависеть от выбора системы координат), то и подынтегральная функция в правой части (17) мы должны заменить истинный скаляр:

дифференциальный оператор (Называется "набла" или ковариантная производная, см. статью Дифференциальная геометрия) определен даже для кривого пространства формуле:
(Называется "набла" или ковариантная производная, см. статью Дифференциальная геометрия) определен даже для кривого пространства формуле:

В случае метрики Минковского:

метрический тензор выражается диагональной матрицей с постоянными коэффициентами, поэтому символы Кристоффеля в формуле (20) равны нулю, чем мы и воспользовались в преобразованиях формулы (19).
Проверим, что "лишние" три слагаемые в (19) не портят равенства (17). Поскольку наша механическая система ограничена в трехмерном пространстве, то мы можем взять достаточно большой трехмерный прямоугольный параллелепипед:

в котором полностью помещается система в розлядуваному интервале времени ( ). Это в частности означает, что за пределами параллелепипеда P (а также на его стенках), тензор энергии-импульса T i j вместе со своими производными
). Это в частности означает, что за пределами параллелепипеда P (а также на его стенках), тензор энергии-импульса T i j вместе со своими производными  превращается в ноль. Поэтому вместо формулы (17) мы можем ограничить область интегрирования параллелепипед P и перейти от кратного до повторного интеграла:
превращается в ноль. Поэтому вместо формулы (17) мы можем ограничить область интегрирования параллелепипед P и перейти от кратного до повторного интеграла:

Если мы в самый внутренний интеграл (23) подставим последний слагаемое формулы (19), то получим ноль:

где интегрирование проводится в четырехмерном пространстве между двумя трехмерными гиперплоскостями.
Формулу (25) нельзя применять в кривом пространстве: во-первых векторы в отдаленных точках нельзя добавлять вследствие неоднозначности параллельного переноса векторов, а во-вторых, неясно чем можно заменить параллельные гиперплоскости в кривом пространстве.
Кроме того, интегральный закон сохранения не накладывает интуитивно-понятного ограничения на движение материи: она, а также энергия и импульс, не может перескакивать с одной точки пространства в отдаленную точку, они могут лишь плавно "перетекать" через соседние точки пространства. Например энергия не может попасть из электростанции в лампочку через оборванные провода. Этим мы словесно описали локальность законов сохранения энергии-импульса.
Обратимся к формулам. В некоторой точке (можно искаженного) пространства-времени выберем систему координат O t x y z, что есть Декартовой в данной точке, и в ней зададим маленький (по сравнению с радиусами кривизны пространства и координатных линий) четырехмерное прямоугольный параллелепипед:

и запишем формулу Остроградского-Гаусса для дивергенции тензора энергии-импульса в этом параллелепипеде:

в этой формуле через обозначена трехмерная "поверхность" параллелепипеда P, состоящую из восьми "граней", а интегрирование по этой поверхности учитывает направление вектора нормали, который направленный наружу параллелепипеда P.
обозначена трехмерная "поверхность" параллелепипеда P, состоящую из восьми "граней", а интегрирование по этой поверхности учитывает направление вектора нормали, который направленный наружу параллелепипеда P.
Две грани, которые мы для наглядности назовем "дном" и "крышкой", является параллелепипедами в трехмерном пространстве x y z, взятыми соответственно в момент времени t (1) и t (2). Тензор энергии-импульса бы убегает внутрь параллелепипеда через "дно" и вытекает через "крышку". Разница интегралов по этим двум "гранях" имеет смысл изменения четыре-вектора энергии-импульса в объеме ? x ? y ? z за время ? t

Очевидно, это изменение должно попасть в трехмерный объем ? x ? y ? z через поверхность этого объема.
Рассмотрим приток энергии через грань x = x (1) площадью ? y ? z за интервал времени ? t:

где S x – плотность потока энергии в направлении оси абсцисс. Сравним это выражение с поверхностным интегралом в правой части формулы (27) по соответствующей трехмерной "боковой" грани параллелепипеда P:

Мы можем определить компоненту тензора энергии-импульса

так, чтобы формулы (29) и (30) соответствовали друг другу. Из формул (15) и (30) следует симметрия части компонент тензора энергии-импульса:

Теперь рассмотрим приток импульса через эту самую грань x = x (1) площадью ? y ? z. Он состоит из двух слагаемых: во-первых, через эту грань протекает материя массой:

которая переносит с собой импульс:

и во-вторых, через эту грань действует момент силы от соседней ячейки пространства через внутренние напряжения вещества (давление):
p_i ^ {(2)} = F_i Delta t = sigma_ {i1} Delta y Delta z Delta t "src =" http://upload.wikimedia.org/math/7/6/c/76c...f8b18e7191d738a. png "/>
Суммарный поток импульса приравняем к потоку соответствующей компоненты тензора энергии-импульса:

Таким образом, мы уже определили все компоненты тензора Энегрия-импульса через величины классической механики, пространственная часть этого тензора равна:

По этой привязки и локального закона сохранения энергии-импульса следует, что "поверхностный" интеграл в левой части (27) равна нулю. Поскольку параллелепипед P может быть размещен в любой точке пространства-времени и может быть бесконечно малым, из равенства нулю правой части (27) следует, что везде дивергенция тензора энергии-импульса равен нулю:

Из выражения для компонент тензора энергии-импульса мы видим, что этот тензор вышел симметричным. И это не случайно. Рассмотрим следующий антисимметричный тензор второго ранга в плоском пространстве Минковского (или в столь малой области искривленного пространства, чтобы кривизну можно вуло не учитывать):

Пространственные компоненты этого тензора, очевидно, равны проекциям классического вектора момента импульса:

Покажем, что если интеграл в правой части (39) распространить на всю "поверхность" четырехмерного параллелепипеда, то в результате получим ноль. Действительно, поверхностный интеграл превращается в интеграл от дивергенции:

а дивергенция превращается в ноль вследствие (38) и симметрии тензора энергии-импульса:
Delta ^ k_j T_ {ik} nabla ^ k T_ {ik} = delta ^ k_i T_ {jk} delta ^ k_j T_ {ik} = T_ {ji} – T_ {ij} = 0 "src = "http://upload.wikimedia.org/math/b/7/2/b72ad232a2c5ff2e673bf58b574a4924.png" />
Равенство нулю "поверхностного" интеграла в левой части (41) можно, аналогично тому, как это было с локальным законом сохранения энергии-импульса, трактовать так: изменение момента импульса в какой области пространства возможна лишь вследствие протекания момента импульса через границу этой области.
Тензор энергии-импульса в общем случае имеет вид:

где W – плотность энергии, S i – поток энергии в направлении, задаваемом координатой i,
 , Где ? i j – тензор в обычном пространстве, которое называют тензором напряжений.
, Где ? i j – тензор в обычном пространстве, которое называют тензором напряжений.Для тензора энергии-импульса справедливо соотношение
 ,
,которое является локальным выражением законов сохранения энергии и импульса.
Очевидна также симметрия тензора энергии-импульса T i j относительно перестановок индексов. Это свойство выражает локальный закон сохранения момента импульса.
Значение тензора энергии-импульса в том, что он входит в основной уравнения общей теории относительности – уравнение Эйнштейна, и, таким образом позволяет дополнить эти уравнения ривннямы состояния вещества.
В классической механике движение непрерывного вещества описывает гидродинамика и теория упругости твердых тел. Каждая частица вещества в точке 3-мерного пространства (x, y, z) и в некоторый момент времени t описывается плотностью:

а также скоростью в этой точке:

и тензором напряжений ? ??, описывающий силовое взаимодействие частицы вещества с соседними частицами.

В случае жидкости или газа, тензор напряжений диагональный и выражается через давление p формуле:

Поскольку вещество "размазана" в пространстве, выделим в какой момент времени (t = t 0) элемент объема ? V. Размер четыре-вектора энергии-импульса ? p ? для части вещества, попавшего в этот объем, пропорциональна самому объема с некоторыми коэффициентами пропорциональности
 :
:
Левая часть этого уравнения есть четыре-вектором. Исследуем, с точки зрения тензорного анализа, что собой представляет произведение в правой части уравнения.
Начнем с трехмерного объема ? V, представив его в виде параллелепипеда, построенного на трех векторах
 . Эти векторы можно считать четыре-векторами, с нулевой первой (временной) координате. Объем является величиной тензора третьего ранга, составленный внешним произведением этих векторов:
. Эти векторы можно считать четыре-векторами, с нулевой первой (временной) координате. Объем является величиной тензора третьего ранга, составленный внешним произведением этих векторов:
Пользуясь единичным антисимметричным тензором, мы можем также составить дуальный четыре-вектор:

где g – детерминант метрического тензора.
В этой формуле множитель мнимой единицы введено для того, чтобы компоненты вектора ? V ? были действительными числами. Величина этого вектора равна объему ? V, а направление ортогональный к составляющим векторов
 . То есть в выбранной системе координат он направлен вдоль оси времени:
. То есть в выбранной системе координат он направлен вдоль оси времени:
Теперь мы можем, меняя при необходимости обозначения коэффициентов
 переписать формулу (7) так:
переписать формулу (7) так:
В этой формуле мы сначала вели еще один индекс "ноль" в обозначении коэффициентов, а потом чисто формально добавили еще три нулевые слагаемые (поскольку согласно (10) пространственные компоненты вектора ? V равны нулю).
Правая часть формулы (11) имеет вид произведению скорости света на свертке тензора второго ранга с вектором. Обозначим тензор
 и назовем его тензором энергии-импульса. Тогда четыре-вектор энергии-импульса вещества, попавшего в элемент объема ? V, согласно формуле (11) запишется в виде свертки тензора энергии-импульса с чотиривектором объема:
и назовем его тензором энергии-импульса. Тогда четыре-вектор энергии-импульса вещества, попавшего в элемент объема ? V, согласно формуле (11) запишется в виде свертки тензора энергии-импульса с чотиривектором объема:
Расписывая покомпонентно формулу (12) и учитывая (6) находим, что если ? = 0


то есть верхний левый элемент матрицы T имеет смысл плотности энергии.
Теперь приравняем индекс ? одной из пространственных координат, например ? = 1. Тогда

Откуда мы можем выразить T 10 двумя способами, учитывая связь импульса с массой ? p 1 = ? m v 1 и формулу Эйнштейна ? E = ? m c 2:

Соответственно имеем две трактовки компоненты T 10: или плотность проекции импульса, умноженная на скорость света, или поток энергии в направлении оси абсцисс, разделенный на скорость света.
В классической механике совокупный импульс системы физических тел и электромагнитного поля сохраняется, т.е. не изменяется со временем. То же касается энергии, если розглядиты действие только консервативных сил. Попробуем выяснить, как эти законы сохранения отражаются в теории относительности на свойствах тензора энергии-импульса.
Начнем с того, что энергия и импульс образуют четыре-вектор (6). Операцию сложения двух пространственно-разнесенных векторов можно осуществить, совершив параллельное перенесение одного вектора в точку нахождения другого. Такая операция будет однозначным только для плоского пространства, с нулевым тензором Римана. Итак начнем с рассмотрения небольшой, ограниченной в пространстве механической системы, гравитационным полем которой (а следовательно и искривлением пространства) можно пренебречь. Для этого надо, чтобы все массы тел были достаточно малыми. Систему координат будем считать прямоугольная декартова.
Выберем фиксированный момент времени t = t (1) i найдем общий четыре-вектор энергии-импульса системы, интегрировать формулу (12) по всему трехмерному пространству (который является гиперплоскостью в четырехмерном пространстве-времени):

В другой момент времени t = t (2) четыре-вектор энергии-импульса останется неизменным, и нулевую разницу мы можем записать в виде интеграла по четырехмерном прослойки между двумя гиперплоскостями:

В последнем интеграле дифференциал d ? является инвариантным элементом четырехмерного объема (см. Интегрирование по объему многообразиях):

Поскольку все физические законы должны носить тензорный характер (а значит не зависеть от выбора системы координат), то и подынтегральная функция в правой части (17) мы должны заменить истинный скаляр:

дифференциальный оператор
 (Называется "набла" или ковариантная производная, см. статью Дифференциальная геометрия) определен даже для кривого пространства формуле:
(Называется "набла" или ковариантная производная, см. статью Дифференциальная геометрия) определен даже для кривого пространства формуле:
В случае метрики Минковского:

метрический тензор выражается диагональной матрицей с постоянными коэффициентами, поэтому символы Кристоффеля в формуле (20) равны нулю, чем мы и воспользовались в преобразованиях формулы (19).
Проверим, что "лишние" три слагаемые в (19) не портят равенства (17). Поскольку наша механическая система ограничена в трехмерном пространстве, то мы можем взять достаточно большой трехмерный прямоугольный параллелепипед:

в котором полностью помещается система в розлядуваному интервале времени (
 ). Это в частности означает, что за пределами параллелепипеда P (а также на его стенках), тензор энергии-импульса T i j вместе со своими производными
). Это в частности означает, что за пределами параллелепипеда P (а также на его стенках), тензор энергии-импульса T i j вместе со своими производными  превращается в ноль. Поэтому вместо формулы (17) мы можем ограничить область интегрирования параллелепипед P и перейти от кратного до повторного интеграла:
превращается в ноль. Поэтому вместо формулы (17) мы можем ограничить область интегрирования параллелепипед P и перейти от кратного до повторного интеграла:
Если мы в самый внутренний интеграл (23) подставим последний слагаемое формулы (19), то получим ноль:

где интегрирование проводится в четырехмерном пространстве между двумя трехмерными гиперплоскостями.
Формулу (25) нельзя применять в кривом пространстве: во-первых векторы в отдаленных точках нельзя добавлять вследствие неоднозначности параллельного переноса векторов, а во-вторых, неясно чем можно заменить параллельные гиперплоскости в кривом пространстве.
Кроме того, интегральный закон сохранения не накладывает интуитивно-понятного ограничения на движение материи: она, а также энергия и импульс, не может перескакивать с одной точки пространства в отдаленную точку, они могут лишь плавно "перетекать" через соседние точки пространства. Например энергия не может попасть из электростанции в лампочку через оборванные провода. Этим мы словесно описали локальность законов сохранения энергии-импульса.
Обратимся к формулам. В некоторой точке (можно искаженного) пространства-времени выберем систему координат O t x y z, что есть Декартовой в данной точке, и в ней зададим маленький (по сравнению с радиусами кривизны пространства и координатных линий) четырехмерное прямоугольный параллелепипед:

и запишем формулу Остроградского-Гаусса для дивергенции тензора энергии-импульса в этом параллелепипеде:

в этой формуле через
 обозначена трехмерная "поверхность" параллелепипеда P, состоящую из восьми "граней", а интегрирование по этой поверхности учитывает направление вектора нормали, который направленный наружу параллелепипеда P.
обозначена трехмерная "поверхность" параллелепипеда P, состоящую из восьми "граней", а интегрирование по этой поверхности учитывает направление вектора нормали, который направленный наружу параллелепипеда P.Две грани, которые мы для наглядности назовем "дном" и "крышкой", является параллелепипедами в трехмерном пространстве x y z, взятыми соответственно в момент времени t (1) и t (2). Тензор энергии-импульса бы убегает внутрь параллелепипеда через "дно" и вытекает через "крышку". Разница интегралов по этим двум "гранях" имеет смысл изменения четыре-вектора энергии-импульса в объеме ? x ? y ? z за время ? t

Очевидно, это изменение должно попасть в трехмерный объем ? x ? y ? z через поверхность этого объема.
Рассмотрим приток энергии через грань x = x (1) площадью ? y ? z за интервал времени ? t:

где S x – плотность потока энергии в направлении оси абсцисс. Сравним это выражение с поверхностным интегралом в правой части формулы (27) по соответствующей трехмерной "боковой" грани параллелепипеда P:

Мы можем определить компоненту тензора энергии-импульса

так, чтобы формулы (29) и (30) соответствовали друг другу. Из формул (15) и (30) следует симметрия части компонент тензора энергии-импульса:

Теперь рассмотрим приток импульса через эту самую грань x = x (1) площадью ? y ? z. Он состоит из двух слагаемых: во-первых, через эту грань протекает материя массой:

которая переносит с собой импульс:

и во-вторых, через эту грань действует момент силы от соседней ячейки пространства через внутренние напряжения вещества (давление):
p_i ^ {(2)} = F_i Delta t = sigma_ {i1} Delta y Delta z Delta t "src =" http://upload.wikimedia.org/math/7/6/c/76c...f8b18e7191d738a. png "/>
Суммарный поток импульса приравняем к потоку соответствующей компоненты тензора энергии-импульса:

Таким образом, мы уже определили все компоненты тензора Энегрия-импульса через величины классической механики, пространственная часть этого тензора равна:

По этой привязки и локального закона сохранения энергии-импульса следует, что "поверхностный" интеграл в левой части (27) равна нулю. Поскольку параллелепипед P может быть размещен в любой точке пространства-времени и может быть бесконечно малым, из равенства нулю правой части (27) следует, что везде дивергенция тензора энергии-импульса равен нулю:

Из выражения для компонент тензора энергии-импульса мы видим, что этот тензор вышел симметричным. И это не случайно. Рассмотрим следующий антисимметричный тензор второго ранга в плоском пространстве Минковского (или в столь малой области искривленного пространства, чтобы кривизну можно вуло не учитывать):

Пространственные компоненты этого тензора, очевидно, равны проекциям классического вектора момента импульса:

Покажем, что если интеграл в правой части (39) распространить на всю "поверхность" четырехмерного параллелепипеда, то в результате получим ноль. Действительно, поверхностный интеграл превращается в интеграл от дивергенции:

а дивергенция превращается в ноль вследствие (38) и симметрии тензора энергии-импульса:
Delta ^ k_j T_ {ik} nabla ^ k T_ {ik} = delta ^ k_i T_ {jk} delta ^ k_j T_ {ik} = T_ {ji} – T_ {ij} = 0 "src = "http://upload.wikimedia.org/math/b/7/2/b72ad232a2c5ff2e673bf58b574a4924.png" />
Равенство нулю "поверхностного" интеграла в левой части (41) можно, аналогично тому, как это было с локальным законом сохранения энергии-импульса, трактовать так: изменение момента импульса в какой области пространства возможна лишь вследствие протекания момента импульса через границу этой области.
 Просмотров: 3940
Просмотров: 3940
 Дата: 19-02-2011
Дата: 19-02-2011
Закон дисперсии
Закон дисперсии – общее название законов зависимости различных физических характеристик от частоты или импульса. Зависимость показателя преломления среды от частоты. Зависимость диэлектрической
ПОДРОБНЕЕ
Теорема Нетер
Теорема Нетер – утверждение в теоретической физике, согласно которому каждой дифференцируемы симметрии соответствует интеграл движения. Например, однородности пространства соответствует закон
ПОДРОБНЕЕ
Уравнения Эйнштейна
Уравнения Эйнштейна – основные уравнения общей теории относительности. Неизвестной величиной в уравнениях Эйнштейна является метрический тензор g i k где R i k – тензор Риччи, R – скалярное
ПОДРОБНЕЕ
4-тензор
4-тензор – математический объект, используемый для описания поля в релятивистской физике, тензор, определенный в четырехмерном пространстве-времени, повороты системы отсчета в котором включают как
ПОДРОБНЕЕ
Законы сохранения
Законы сохранения в физике – это группа законов, которые утверждают, что значение определенных физических величин не меняется в замкнутой системе с ее эволюцией. Далее приводится частичный перечень
ПОДРОБНЕЕ