4-тензор
4-тензор – математический объект, используемый для описания поля в релятивистской физике, тензор, определенный в четырехмерном пространстве-времени, повороты системы отсчета в котором включают как обычные повороты трехмерного пространства, так и переход между системами отсчета, движущихся с различными скоростями одна относительно другой.
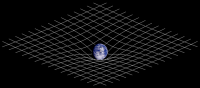
В загальтому случае 4-тензор является объектом с набором индексов:
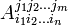
При изменении системы отсчета компоненты этого объекта превращаются по закону
 ,
,
где ? i j – матрица поворота, ? i j – обратная ей.
Верхние индексы называются котравариатнимы, нижние – ковариантный. Суммарное число индексов задает ранг тензора. 4-вектор является 4-тензором первого ранга.
Обычно в физике тензоры одинаковой природы с разным числом ковариантных и контравариантных индексов считаются родственными (дуальными). Опускания или поднятия индеска осуществляется с помощью метрического тензора , Например для 4-тензора второго ранга
, Например для 4-тензора второго ранга

Уравнения теории относительности особенно удобно записывать, используя 4-векторы и 4-тензоры. Главным преимуществом такой записи является то, что в этой форме уравнения автоматически лоренц-инвариантны, то есть не изменяются при переходе от одной инерциальной системы координат в другую.
4-Терзора электромагнитного поля
Подробнее в статье 4-тензор электромагнитного поля
Соответствующий 4-тензор существует также и для описания электромагнитного поля. Это 4-тензор второго ранга. При его использовании основные уравнения для электромагнитного поля: уравнения Максвелла и уравнение движения заряженной частицы в поле имеют особенно простую и элегантную форму.
Определение через 4-потенциал
4-тензор определяется через производные от 4-потенциала:
 .
.
Определение через трехмерные векторы
4-тензор определяется через обычные трехмерные составные векторов напряженности следующим образом:


Первая форма – это ковариантный тензор, вторая форма – контравариантный тензор.
Сила Лоренца
Записанное в 4-векторной форме уравнение движения заряженной частицы в электромагнитном поле принимает вид
 ,
,
где u k – 4-скорость, q – электрический заряд частицы, c – скорость света, m – масса покоя. Правая часть этого уравнения это сила Лоренца.
В загальтому случае 4-тензор является объектом с набором индексов:
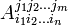
При изменении системы отсчета компоненты этого объекта превращаются по закону
 ,
,где ? i j – матрица поворота, ? i j – обратная ей.
Верхние индексы называются котравариатнимы, нижние – ковариантный. Суммарное число индексов задает ранг тензора. 4-вектор является 4-тензором первого ранга.
Обычно в физике тензоры одинаковой природы с разным числом ковариантных и контравариантных индексов считаются родственными (дуальными). Опускания или поднятия индеска осуществляется с помощью метрического тензора
 , Например для 4-тензора второго ранга
, Например для 4-тензора второго ранга
Уравнения теории относительности особенно удобно записывать, используя 4-векторы и 4-тензоры. Главным преимуществом такой записи является то, что в этой форме уравнения автоматически лоренц-инвариантны, то есть не изменяются при переходе от одной инерциальной системы координат в другую.
4-Терзора электромагнитного поля
Подробнее в статье 4-тензор электромагнитного поля
Соответствующий 4-тензор существует также и для описания электромагнитного поля. Это 4-тензор второго ранга. При его использовании основные уравнения для электромагнитного поля: уравнения Максвелла и уравнение движения заряженной частицы в поле имеют особенно простую и элегантную форму.
Определение через 4-потенциал
4-тензор определяется через производные от 4-потенциала:
 .
.Определение через трехмерные векторы
4-тензор определяется через обычные трехмерные составные векторов напряженности следующим образом:


Первая форма – это ковариантный тензор, вторая форма – контравариантный тензор.
Сила Лоренца
Записанное в 4-векторной форме уравнение движения заряженной частицы в электромагнитном поле принимает вид
 ,
,где u k – 4-скорость, q – электрический заряд частицы, c – скорость света, m – масса покоя. Правая часть этого уравнения это сила Лоренца.
 Просмотров: 3031
Просмотров: 3031
 Дата: 19-02-2011
Дата: 19-02-2011
Теорема Нетер
Теорема Нетер – утверждение в теоретической физике, согласно которому каждой дифференцируемы симметрии соответствует интеграл движения. Например, однородности пространства соответствует закон
ПОДРОБНЕЕ
Тензор энергии-импульса
Тензор энергии-импульса – симметричный 4-тензор, определенный в пространстве-времени, который одновременно задает плотность энергии и ее потоков и определяет закон изменения этих величин при переходе
ПОДРОБНЕЕ
Метрика пространства-времени
Схематическое двумерных изображений искривления пространства-времени около массивного тела Метрика пространства-времени – 4-тензор, который определяет свойства пространства-времени в общей теории
ПОДРОБНЕЕ
Тензоры Эйнштейна и Риччи
Наряду с серией кривизн Гаусса m-й степени: естественно появляются (смотрите статью Интегралы Гаусса) следующие две серии тензоров второго ранга. Тензор Эйнштейна m-й степени: и тензоры Риччи m-й
ПОДРОБНЕЕ
Тензор кривизны
Тензор кривизны (Тензор внутренней кривизны многообразиях) появляется при рассмотрении коммутатора ковариантных производных ковариантного вектора (смотрите статью Дифференциальная геометрия) Вместо
ПОДРОБНЕЕ
Пространство-время
Двумерная иллюстрация искривления пространства-времени вблизи массивного тела Пространство-время – искусственный математический 4-измеримое пространство событий. Положение любого события в
ПОДРОБНЕЕ