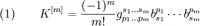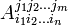Тензор кривизны
Тензор кривизны  (Тензор внутренней кривизны многообразиях) появляется при рассмотрении коммутатора ковариантных производных ковариантного вектора (смотрите статью Дифференциальная геометрия)
(Тензор внутренней кривизны многообразиях) появляется при рассмотрении коммутатора ковариантных производных ковариантного вектора (смотрите статью Дифференциальная геометрия)


Вместо ковариантных компонент a i можно подставить базисные векторы :
:

И учитывая, что ковариантная производная от базисных векторов равна векторам полной кривизны
равна векторам полной кривизны  (Смотрите Простые вычисления дифференциальной геометрии), имеем:
(Смотрите Простые вычисления дифференциальной геометрии), имеем:

Домножим формулу (3) скалярно на , I учтем ортогональность векторов кривизны до многообразия:
, I учтем ортогональность векторов кривизны до многообразия:  . В результате получаем формулу для ковариантных компонент тензора Римана:
. В результате получаем формулу для ковариантных компонент тензора Римана:



или после смены знака и переименование индексов:

Как можно увидеть из последнего уравнения (в скалярных произведениях индексы k и l переставлены), тензор Римана антисимметричный по первой паре индексов i j и по второй паре индексов k l (при перестановке уменьшающееся и вычитаемое в правой части формулы (4) меняются местами) :

Также легко видеть, что тензор Римана не меняется при перестановке первой пары индексов i j со второй парой индексов k l (при перестановке в множителях уменьшаемого индексы переставляются, но поскольку величины симметричные по индексам, то скалярное произведение уменьшаемого не изменится; в вычитаемое аналогично, но сомножители в скалярном произведении меняются местами, не влияет на результат):
симметричные по индексам, то скалярное произведение уменьшаемого не изменится; в вычитаемое аналогично, но сомножители в скалярном произведении меняются местами, не влияет на результат):

Свертка тензора Римана по первому и третьему индексам (или, что эквивалентно, по второму и четвертому индексах) дает симметричный тензор второго ранга R i k, который называется тензором Риччи:

Тензор Риччи симметричен:

Тензор Риччи можно свернуть по индексам, получив скалярную кривизну:

Учитывая (4), имеем:

Коммутатор для контравариантный векора получаем, подняв индекс i в формуле (1):

Поскольку коммутатор ковариантных производных действует на произведение тензоров T U по правилу дифференциального оператора:
действует на произведение тензоров T U по правилу дифференциального оператора:

то мы можем, пользуясь формулами (1) и (11), вычислить действие коммутатора ковариантных производных на тензор, который является произведением векторов.
Но произвольный тензор можно представить линейной комбинацией таких элементарных тензоров, поэтому при действии коммутатора на произвольный тензор с любым количеством верхних и нижних индексов, имеем:

Тензор Римана удовлетворяющие двум тождества Бианки.
Алгебраическая тождество Бианки (циклическая перестановка индексов i j k):

Дифференциальная тождество Бианки (циклическая перестановка индексов p j k):

 (Тензор внутренней кривизны многообразиях) появляется при рассмотрении коммутатора ковариантных производных ковариантного вектора (смотрите статью Дифференциальная геометрия)
(Тензор внутренней кривизны многообразиях) появляется при рассмотрении коммутатора ковариантных производных ковариантного вектора (смотрите статью Дифференциальная геометрия)

Вместо ковариантных компонент a i можно подставить базисные векторы
 :
:
И учитывая, что ковариантная производная от базисных векторов
 равна векторам полной кривизны
равна векторам полной кривизны  (Смотрите Простые вычисления дифференциальной геометрии), имеем:
(Смотрите Простые вычисления дифференциальной геометрии), имеем:
Домножим формулу (3) скалярно на
 , I учтем ортогональность векторов кривизны до многообразия:
, I учтем ортогональность векторов кривизны до многообразия:  . В результате получаем формулу для ковариантных компонент тензора Римана:
. В результате получаем формулу для ковариантных компонент тензора Римана:


или после смены знака и переименование индексов:

Как можно увидеть из последнего уравнения (в скалярных произведениях индексы k и l переставлены), тензор Римана антисимметричный по первой паре индексов i j и по второй паре индексов k l (при перестановке уменьшающееся и вычитаемое в правой части формулы (4) меняются местами) :

Также легко видеть, что тензор Римана не меняется при перестановке первой пары индексов i j со второй парой индексов k l (при перестановке в множителях уменьшаемого индексы переставляются, но поскольку величины
 симметричные по индексам, то скалярное произведение уменьшаемого не изменится; в вычитаемое аналогично, но сомножители в скалярном произведении меняются местами, не влияет на результат):
симметричные по индексам, то скалярное произведение уменьшаемого не изменится; в вычитаемое аналогично, но сомножители в скалярном произведении меняются местами, не влияет на результат):
Свертка тензора Римана по первому и третьему индексам (или, что эквивалентно, по второму и четвертому индексах) дает симметричный тензор второго ранга R i k, который называется тензором Риччи:

Тензор Риччи симметричен:

Тензор Риччи можно свернуть по индексам, получив скалярную кривизну:

Учитывая (4), имеем:

Коммутатор для контравариантный векора получаем, подняв индекс i в формуле (1):

Поскольку коммутатор ковариантных производных
 действует на произведение тензоров T U по правилу дифференциального оператора:
действует на произведение тензоров T U по правилу дифференциального оператора:
то мы можем, пользуясь формулами (1) и (11), вычислить действие коммутатора ковариантных производных на тензор, который является произведением векторов.
Но произвольный тензор можно представить линейной комбинацией таких элементарных тензоров, поэтому при действии коммутатора на произвольный тензор с любым количеством верхних и нижних индексов, имеем:

Тензор Римана удовлетворяющие двум тождества Бианки.
Алгебраическая тождество Бианки (циклическая перестановка индексов i j k):

Дифференциальная тождество Бианки (циклическая перестановка индексов p j k):

 Просмотров: 3221
Просмотров: 3221
 Дата: 19-02-2011
Дата: 19-02-2011
Дифференциальная геометрия
Дифференциальная геометрия – это математическая дисциплина применяющая методы математического анализа для изучения гладких кривых, поверхностей и, в общем виде, их n-мерных аналогов, которые
ПОДРОБНЕЕ
Уравнения Эйнштейна
Уравнения Эйнштейна – основные уравнения общей теории относительности. Неизвестной величиной в уравнениях Эйнштейна является метрический тензор g i k где R i k – тензор Риччи, R – скалярное
ПОДРОБНЕЕ
Многообразие
Многообразие – это объект, который локально имеет характер метрического пространства размерности n. Он имеет целочисленных размерность, которая указывает сколькими параметрами (координатами) можно
ПОДРОБНЕЕ
Тензоры Эйнштейна и Риччи
Наряду с серией кривизн Гаусса m-й степени: естественно появляются (смотрите статью Интегралы Гаусса) следующие две серии тензоров второго ранга. Тензор Эйнштейна m-й степени: и тензоры Риччи m-й
ПОДРОБНЕЕ
Метрический тензор
Величины, которые касаются геометрии – это расстояния, длины кривых, площади и объемы (в том числе m-мерные объемы) геометрических фигур, а также углы между векторами, прямыми и т.д. Рассмотрим
ПОДРОБНЕЕ