Тензоры Эйнштейна и Риччи
Наряду с серией кривизн Гаусса m-й степени:
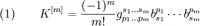
естественно появляются (смотрите статью Интегралы Гаусса) следующие две серии тензоров второго ранга.
Тензор Эйнштейна m-й степени:

и тензоры Риччи m-й степени:

Из формул (2) и (3) легко видеть, что неполная свертка тензора Эйнштейна с тензором полной кривизны гиперповерхности равна тензора Риччи на единицу большего степени:

Легко также вычислить след (свертку) тензора Риччи:

Несколько сложнее вычислять след тензора Эйнштейна. Для этого надо воспользоваться следующим свойством тензора метрической матрешки:

В результате имеем:

Поскольку тензор метрической матрешки перестановочных с ковариантной производной, то мы можем записать:

Первое слагаемое в сумме симметричный по индексам (i, s 1) вследствие уравнения Петерсона-Кодацци (смотрите статью гиперповерхности):

Для вывода следующих формул, связывают тензоры Эйнштейна и Риччи, надо вывести формулу, как тензор метрической матрешки (что по определению равна определителю матрицы, составленной из дельта-символов) раскладывается по первой строке матрицы.
Пусть мы имеем тензор метрической матрешки 2 (m + 1) ранга, который записывается в виде определителя матрицы размером . Запишем его расписание по первой строке:
. Запишем его расписание по первой строке:


В правой части этой формулы матрицы определителей слагаемых образуются в результате вычеркивания из матрицы разложения первой строки и соответственно первого, второго, третьего … столбцов. Знаки слагаемых чередуются. Формулу (10) можно записать также в обозначении тензора метрической матрешки:
матрицы определителей слагаемых образуются в результате вычеркивания из матрицы разложения первой строки и соответственно первого, второго, третьего … столбцов. Знаки слагаемых чередуются. Формулу (10) можно записать также в обозначении тензора метрической матрешки:
p_1 dots p_m} dots + (-1) ^ {m-1} delta ^ i_ {p_m} g ^ {s_1 s_2 dots s_m} _ {j, p_1 dots p_ {m-1}} "src =" http://upload.wikimedia.org/math/3/d/8/3d8...7651f223c12.png "/>
Посмотрим внимательнее на первые три слагаемые, обращая внимание на соответствие верхних и нижних индексов тензора метрической матрешки. Первые два слагаемых в этом смысле удовлетворительные. Что касается третьего слагаемого, то формула станет в некотором смысле симетричнишою, если в тензора метричои матрешки мы переставим местами (с соответствующим изменением знака слагаемого) нижние индексы (j, p 1). Сделаем аналогичные изменения и для остальных слагаемых. В результате имеем следующую формулу:

В этой формуле первое слагаемое стоит со знаком "плюс", а остальные m слагаемых со знаком "минус". Попутно отметим, что из формулы (11) легко следует формула свертки (6).
Можно получить еще одну формулу, аналогичную (11), если раскладывать определитель не по строке, а по столбцу:

Подставим разложение (12) в формулу (2). Получаем:

При вскрытии скобок первое слагаемое дает в результате свертки

а остальные слагаемых, вследствие симметрии тензора метрической матрешки относительно перестановки "вертикальных" пар индексов, каждый дает одинаковый результат:

Поскольку количество слагаемых (14) в правой части формулы (13) равна m, то имеем:
R ^ {[m] i} _j – K ^ {[m]} delta ^ i_j "src =" http://upload.wikimedia.org/math/8/d/6/8d6...245f1bf0651.png "/>
Поскольку согласно формуле (15) тензор Риччи отличается от тензора Эйнштейна добавлением симметричного тензора K [m] g i j, то нам достаточно доказать симметрию только одного, например тензора Эйнштейна. Жонглируя индексами (поднимая и опуская) в формуле (2), находим для коваиантних координат тензора Эйнштейна:

Поскольку тензор b i j симметричный, то мы можем в тензора метрической матрешки в формуле (16) переставить каждый индекс s i с соответствующим ему индексом p i:

Далее, тензор метрической матрешки симметричный относительно групп индексов. Переставляя группы индексов в Тезора метрической матрешки формулы (17), мы придем к правой части формулы (16) с переставленными индексами i, j. Следовательно

Аналогично тому, как это мы вычисляли для кривизн Гаусса, находим:


Следовательно для четных степеней тензоры Эйнштейна и Риччи являются объектами внутренней геометрии, а потому определенные для всех многообразий, а не только для гиперповерхонь.
Интересно, что все основные свойства тензоров Эйнштейна и Риччи (нулевая дивергенция тензора Эйнштейна, основной связь между тензором Эйнштейна и тензором Риччи, их симметрия) сохраняются для всех многообразий, если для их вывода пользоваться формулами (19), (20). Например вычислим дивергенцию тензора Эйнштейна:
Cdots "src =" http://upload.wikimedia.org/math/4/b/7/4b7...391100dc410.png "/>
Здесь выписаны только первое слагаемое от производной произведения, остальные слагаемых (с производными следующих сомножителей) аналогичны. В этом слагаемого обратим внимание на три индекса i, s 1, p 1 по которым ведется свертка. Эти три индекса попарно различны, поскольку они входят в одну антисимметрична группу индексов метрической матрешки, и в ходе свертки перебираются все перестановки (в том числе циклические) этих индексов. Но для тензора Римана сумма циклических перестановок равна нулю вследствие дифференциальной тождества Бианки:

поэтому первое слагаемое в правой части формулы (21) равна нулю. Для остальных слагаемых аналогично.
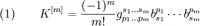
естественно появляются (смотрите статью Интегралы Гаусса) следующие две серии тензоров второго ранга.
Тензор Эйнштейна m-й степени:

и тензоры Риччи m-й степени:

Из формул (2) и (3) легко видеть, что неполная свертка тензора Эйнштейна с тензором полной кривизны гиперповерхности равна тензора Риччи на единицу большего степени:

Легко также вычислить след (свертку) тензора Риччи:

Несколько сложнее вычислять след тензора Эйнштейна. Для этого надо воспользоваться следующим свойством тензора метрической матрешки:

В результате имеем:

Поскольку тензор метрической матрешки перестановочных с ковариантной производной, то мы можем записать:

Первое слагаемое в сумме симметричный по индексам (i, s 1) вследствие уравнения Петерсона-Кодацци (смотрите статью гиперповерхности):

Для вывода следующих формул, связывают тензоры Эйнштейна и Риччи, надо вывести формулу, как тензор метрической матрешки (что по определению равна определителю матрицы, составленной из дельта-символов) раскладывается по первой строке матрицы.
Пусть мы имеем тензор метрической матрешки 2 (m + 1) ранга, который записывается в виде определителя матрицы размером
 . Запишем его расписание по первой строке:
. Запишем его расписание по первой строке:

В правой части этой формулы
 матрицы определителей слагаемых образуются в результате вычеркивания из матрицы разложения первой строки и соответственно первого, второго, третьего … столбцов. Знаки слагаемых чередуются. Формулу (10) можно записать также в обозначении тензора метрической матрешки:
матрицы определителей слагаемых образуются в результате вычеркивания из матрицы разложения первой строки и соответственно первого, второго, третьего … столбцов. Знаки слагаемых чередуются. Формулу (10) можно записать также в обозначении тензора метрической матрешки:p_1 dots p_m} dots + (-1) ^ {m-1} delta ^ i_ {p_m} g ^ {s_1 s_2 dots s_m} _ {j, p_1 dots p_ {m-1}} "src =" http://upload.wikimedia.org/math/3/d/8/3d8...7651f223c12.png "/>
Посмотрим внимательнее на первые три слагаемые, обращая внимание на соответствие верхних и нижних индексов тензора метрической матрешки. Первые два слагаемых в этом смысле удовлетворительные. Что касается третьего слагаемого, то формула станет в некотором смысле симетричнишою, если в тензора метричои матрешки мы переставим местами (с соответствующим изменением знака слагаемого) нижние индексы (j, p 1). Сделаем аналогичные изменения и для остальных слагаемых. В результате имеем следующую формулу:

В этой формуле первое слагаемое стоит со знаком "плюс", а остальные m слагаемых со знаком "минус". Попутно отметим, что из формулы (11) легко следует формула свертки (6).
Можно получить еще одну формулу, аналогичную (11), если раскладывать определитель не по строке, а по столбцу:

Подставим разложение (12) в формулу (2). Получаем:

При вскрытии скобок первое слагаемое дает в результате свертки

а остальные слагаемых, вследствие симметрии тензора метрической матрешки относительно перестановки "вертикальных" пар индексов, каждый дает одинаковый результат:

Поскольку количество слагаемых (14) в правой части формулы (13) равна m, то имеем:
R ^ {[m] i} _j – K ^ {[m]} delta ^ i_j "src =" http://upload.wikimedia.org/math/8/d/6/8d6...245f1bf0651.png "/>
Поскольку согласно формуле (15) тензор Риччи отличается от тензора Эйнштейна добавлением симметричного тензора K [m] g i j, то нам достаточно доказать симметрию только одного, например тензора Эйнштейна. Жонглируя индексами (поднимая и опуская) в формуле (2), находим для коваиантних координат тензора Эйнштейна:

Поскольку тензор b i j симметричный, то мы можем в тензора метрической матрешки в формуле (16) переставить каждый индекс s i с соответствующим ему индексом p i:

Далее, тензор метрической матрешки симметричный относительно групп индексов. Переставляя группы индексов в Тезора метрической матрешки формулы (17), мы придем к правой части формулы (16) с переставленными индексами i, j. Следовательно

Аналогично тому, как это мы вычисляли для кривизн Гаусса, находим:


Следовательно для четных степеней тензоры Эйнштейна и Риччи являются объектами внутренней геометрии, а потому определенные для всех многообразий, а не только для гиперповерхонь.
Интересно, что все основные свойства тензоров Эйнштейна и Риччи (нулевая дивергенция тензора Эйнштейна, основной связь между тензором Эйнштейна и тензором Риччи, их симметрия) сохраняются для всех многообразий, если для их вывода пользоваться формулами (19), (20). Например вычислим дивергенцию тензора Эйнштейна:
Cdots "src =" http://upload.wikimedia.org/math/4/b/7/4b7...391100dc410.png "/>
Здесь выписаны только первое слагаемое от производной произведения, остальные слагаемых (с производными следующих сомножителей) аналогичны. В этом слагаемого обратим внимание на три индекса i, s 1, p 1 по которым ведется свертка. Эти три индекса попарно различны, поскольку они входят в одну антисимметрична группу индексов метрической матрешки, и в ходе свертки перебираются все перестановки (в том числе циклические) этих индексов. Но для тензора Римана сумма циклических перестановок равна нулю вследствие дифференциальной тождества Бианки:

поэтому первое слагаемое в правой части формулы (21) равна нулю. Для остальных слагаемых аналогично.
 Просмотров: 3466
Просмотров: 3466
 Дата: 19-02-2011
Дата: 19-02-2011
Теорема Нетер
Теорема Нетер – утверждение в теоретической физике, согласно которому каждой дифференцируемы симметрии соответствует интеграл движения. Например, однородности пространства соответствует закон
ПОДРОБНЕЕ
Уравнения Эйнштейна
Уравнения Эйнштейна – основные уравнения общей теории относительности. Неизвестной величиной в уравнениях Эйнштейна является метрический тензор g i k где R i k – тензор Риччи, R – скалярное
ПОДРОБНЕЕ
Метрический тензор
Величины, которые касаются геометрии – это расстояния, длины кривых, площади и объемы (в том числе m-мерные объемы) геометрических фигур, а также углы между векторами, прямыми и т.д. Рассмотрим
ПОДРОБНЕЕ
Тензор кривизны
Тензор кривизны (Тензор внутренней кривизны многообразиях) появляется при рассмотрении коммутатора ковариантных производных ковариантного вектора (смотрите статью Дифференциальная геометрия) Вместо
ПОДРОБНЕЕ
4-тензор
4-тензор – математический объект, используемый для описания поля в релятивистской физике, тензор, определенный в четырехмерном пространстве-времени, повороты системы отсчета в котором включают как
ПОДРОБНЕЕ
Гравитационные волны
Одним из выводов уравнения Эйнштейна для гравитационного поля: является существование гравитационных волн. Эти волны имеют обычно очень малую амплитуду, исключением может быть разве что экзотический
ПОДРОБНЕЕ