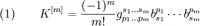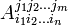Уравнения Эйнштейна
Уравнения Эйнштейна – основные уравнения общей теории относительности. Неизвестной величиной в уравнениях Эйнштейна является метрический тензор g i k

где R i k – тензор Риччи, R – скалярное искажения, g i k – метрический тензор, ? – космологическая константа, T i k – тензор энергии-импульса, который определяет негравитуючу материю, энергию и силы в произвольной точке пространства-времени, ? – число пи, c – скорость света, G – гравитационная постоянная, которая появляется и в соответствующем законе всемирного тяготения Ньютона. Тензор Риччи, скалярное искажения и тензор энергии-импульса тоже зависят от метрического тензора.
В общем случае уравнения Эйнштейна содержит космологическую константу, хотя позже Эйнштейн видпмовився от ее использования. Космологическая константа была введена для того, чтобы достичь стационарности Вселенной, но открытие красного смещения заложило сомнения в стационарности.
Информация о распределении масс и полей содержится в тензора энергии-импульса. Для полного рассмотрения физической системы уравнения Эйнштейна должны быть дополненными уравнением состояния материи.
Попробуем вывести уравнения гравитации, которое согласовывалось с принципами общей теории относительности и в предельном случае малых масс и малых скоростей переходило в классический закон Всемирного тяготения Ньютона. Для вывода достаточно рассмотреть только статическую задачу, когда массы не двигаются и гравитационное поле не меняется со временем. В классическом случае ускорение свободного падения к тяготея центра m дается формулой обратных квадратов:
к тяготея центра m дается формулой обратных квадратов:

Эта сила оказывается консервативной, и аналогично электростатики мы можем рассматривать гравитационный потенциал ?:

Ускорение свободного падения равен взятому со знаком минус градиента потенциала:

а из формулы (3), полностью аналогично электростатики, получаем следующее уравнение Лапласа:

где ? – плотность массы. Это уравнение классической механики мы возьмем за основу и попробуем найти его релятивистский аналог.
При переходе к общей теории относительности мы должны заменить плотность массы ? релятивистски-инвариантной величиной. Такой величиной, причем примерно пропорциональным плотности ?, является тензор энергии-импульса T i j. Поскольку массы неподвижны, то потока энергии нет, и недиагональные элементы Тезора T i j равны нулю. Также мы можем пренебречь напряжениями внутри физического тела по сравнению с очень большой плотностью энергии покоя W = ? c 2. Таким образом, в нашем случае в тензора энергии-импульса отлична от нуля лишь одна временная компонента:

Этот тензор стоять (с некоторым коэффициентом пропорциональности) в правой части искомого уравнения – он порождает гравитацию. А что мы должны написать в левой части, т.е. такое гравитация? Ответ дал Эйнштейн, сформулировав принцип эквивалентности – это искривление четырехмерного пространства-времени. Сила тяжести вычисляется по той же формуле, что и силы инерции в неинерциальных системах координат:

Согласно ковариантная координата силы тяжести в трехмерном пространстве (знак минус учитывает псевдоевклидовисть):

В этой формуле производная координат берется по собственному времени ? материальной точки:

Мы возьмем для измерения силы тяжести недвижимое пробное тело массой m. Вдоль мировой линии этого тела зминюется только нулевая координата , Поэтому:
, Поэтому:

Приравнивая формулы (4) и (9) находим, что нулевая компонента метрического тензора связана с гравитационным потенциалом:

Константу интегрирования мы можем найти, зная что на бесконечности (вдали от тяготея тел) нулевая компонента метрического тензора равна единице, а потенциал превращается в ноль согласно формуле (3). Итак:

Теперь мы готовы подобрать релятивистский аналог для левой части формулы (5). Ясно, что этот аналог должен содержать вторую производную метрического тензора g i j и одновременно быть тензором, чтобы удовлетворить основное требование общей теории относительности – быть инвариантным относительно произвольной замены системы координат. Мы не можем использовать частные производные сами по себе, поскольку они не являются тензором (при замене системы координат преобразуются не по тензорным правилам. Также мы не можем воспользоваться ковариантной производной, поскольку известно, что ковариантная производная метрического тензора
сами по себе, поскольку они не являются тензором (при замене системы координат преобразуются не по тензорным правилам. Также мы не можем воспользоваться ковариантной производной, поскольку известно, что ковариантная производная метрического тензора  тождественно равна нулю. Но нам подходит тензор внутренней кривизны (тензор Римана):
тождественно равна нулю. Но нам подходит тензор внутренней кривизны (тензор Римана):


Ясно, что при малом искривлении пространства-времени мы можем выбрать близкую к декартовой системе координат. В ней символы Кристоффеля будут близки к нулю, так отбросив (два последних) квадратичные слагаемые в формуле (13) мы в правой части получим сумму вторых производных от метрического тензора. В этой сумме также будут приситни вторая производная от g 00, т.е. от гравитационного потенциала (формула 11).
Тензор кривизны R p i j k имеет четыре индекса, поэтому мы не можем его непосредственно приравнивать к тензора энергии-импульса T i j с двумя индексами. Уменьшить количество индексов можно, рассматривая линейные комбинации компонент тензора Римана (12). Очевидно, эти линейные комбинации тоже содержат сумму дугих производных от гравитационного потенциала ? (так что остается надежда получить аналог левой части формулы (5)). Мы не будем вводить новых физических величин, а воспользуемся для коэффициентов этих линейных комбинаций самым метрическим тензором – то есть рассмотрим свертки тензора Римана. Однократная свертка тензора по индексам (s j) дает тензор Риччи R_ {ik}:
по индексам (s j) дает тензор Риччи R_ {ik}:

Этот тензор симметричен и имеет два индекса, как и в тензора энергии-импульса T i j. Но кроме (14) мы можем образовать еще один симметричный тензор, умножив метрический тензор g i j на скалярную кривизну R, которая является сверткой тензора Риччи:

Итак естественными кандидатами на релятивистское обобщение уравнения (5) есть такие линейные комбинации:

где коэффициенты (?, ?, k) являются константами. Эти коэффициенты можно уточнить, воспользовавшись локальным законом сохранения энергии-импульса:

Итак дивергенция от левой части формулы (16) должна равняться нулю. Если бы тензор Римана был совсем произвольным, то добиться нулевой дивергенции мы не смогли бы ни при каких ненулевых константах (?, ?). Но к счастью, как чисто математическая свойство, ковариантные производные тензора Римана связанные дифференциальной тождеством Бианки:

Свернем эту тождественность сначала по индексам (k, q), а затем по (j, p):


Из последнего равенства, переименовав индекс, по которому проходит свертка, мы можем выразить дивергенцию тензора Риччи через градиент скалярной кривизны
через градиент скалярной кривизны  :
:

Теперь мы готовы, чтобы применить дивергенцию к уравнению (16):

Это равенство (закон сохранения энергии-импульса) будет тождественно выполняется, если коэффициент ? равен:

Ясно, что теперь коэффициент ? не может равняться нулю (иначе с учетом (23) и (16) тензор T i j был бы тождественным нулем). Делим равенство (16) на ? и перепозначимо пока неизвестную константу k. В результате приходим к такому уравнения гравитации:

Нам осталось найти константу k. Для этого надо показать, что в приближении слабого поля, левая часть уравнения (24) равна с некоторым коэффициентом лапласиана гравитационного потенциала и вычислить этот коэффициент. Это не совсем тривиально, поскольку кроме временной компоненты g 00 метрического тензора (формула 11), остальные компонент может также меняться. Детали вычисления смотрите в статье Слабое гравитационное поле.
и вычислить этот коэффициент. Это не совсем тривиально, поскольку кроме временной компоненты g 00 метрического тензора (формула 11), остальные компонент может также меняться. Детали вычисления смотрите в статье Слабое гравитационное поле.
Выражение в левой части уравнения (24) является тензором Эйнштейна второй степени:

который можно получить вариацией интеграла Гаусса:

при изменении метрического тензора g i j на малую величину ? g i j. Кривизна Гаусса второй степерня K [2] равна половине скалярной кривизны:

Поскольку для материи (в частности для электромагнитного поля) тензор энергии-импульса тоже образуется из лагранжиана подобным образом как коэффициент при вариации метрики, например:

то отнимая от (28) предварительно умноженное уравнения (26) (с должным множителем, обратным к коэффициенту в правой части уравнения (1)) получим совокупный лагранжиан материи и гравитационного поля:

при вариации которого получается все: как уравнения Эйнштейна для гравитации, так и уравнения движения материи:

Второе слагаемое в правой части (29) является лагранжианом гравитационного поля:

Вариационный принцип встречается не только здесь, но во всех основных разделах физики: классической механике, квантовой механике, электродинамике, теории относительности. Такая распространенность наводит на мысль, что все законы физики связаны неким (еще неизвестным науке) одним универсальным уравнением. Это уравнение может образовываться вариацией "всеобщей действия" от некоторого общего лагранжиана. Сам Альберт Эйнштейн занимался поисками этого уравнения, хотя без значительных успехов. Одним из результатов Эйнштейна является поправка с космологической постоянной.
Рассмотрим вместо выражения (31) любую функцию от тензора Римана и его ковариантных производных, которая образует скаляр по тензорным правилам. Например:

Тогда при вариации этого обобщенного лагранжиана мы получим Обобщенный тензор Эйнштейна. Он подражает основные свойства тензора Эйнштейна (формула 25) второй степени: симметричный, релятивистски инвариантный, нулевая дивергенция. Единственное условие на поправки в формуле (32): они должны быть малыми в масштабах ближнего космоса (т.е. Солнечной системы), чтобы выполнялся закон тяготения Ньютона. Но в других масштабах они могут проявиться. В частности члены с при больших масштабах – вселенских и галактических. Квадратичные члены с
при больших масштабах – вселенских и галактических. Квадратичные члены с  могут проявиться в малых, в частности микроскопических масштабах. Подробнее это описано в статье Поправки к уравнению Эйнштейна.
могут проявиться в малых, в частности микроскопических масштабах. Подробнее это описано в статье Поправки к уравнению Эйнштейна.
Уравнения Эйнштейна нелинейные и развязки можно найти в очень ограниченном количестве случаев. Известнейший развязок – метрика Шварцшильда для сферического распределения массы.

где R i k – тензор Риччи, R – скалярное искажения, g i k – метрический тензор, ? – космологическая константа, T i k – тензор энергии-импульса, который определяет негравитуючу материю, энергию и силы в произвольной точке пространства-времени, ? – число пи, c – скорость света, G – гравитационная постоянная, которая появляется и в соответствующем законе всемирного тяготения Ньютона. Тензор Риччи, скалярное искажения и тензор энергии-импульса тоже зависят от метрического тензора.
В общем случае уравнения Эйнштейна содержит космологическую константу, хотя позже Эйнштейн видпмовився от ее использования. Космологическая константа была введена для того, чтобы достичь стационарности Вселенной, но открытие красного смещения заложило сомнения в стационарности.
Информация о распределении масс и полей содержится в тензора энергии-импульса. Для полного рассмотрения физической системы уравнения Эйнштейна должны быть дополненными уравнением состояния материи.
Попробуем вывести уравнения гравитации, которое согласовывалось с принципами общей теории относительности и в предельном случае малых масс и малых скоростей переходило в классический закон Всемирного тяготения Ньютона. Для вывода достаточно рассмотреть только статическую задачу, когда массы не двигаются и гравитационное поле не меняется со временем. В классическом случае ускорение свободного падения
 к тяготея центра m дается формулой обратных квадратов:
к тяготея центра m дается формулой обратных квадратов:
Эта сила оказывается консервативной, и аналогично электростатики мы можем рассматривать гравитационный потенциал ?:

Ускорение свободного падения равен взятому со знаком минус градиента потенциала:

а из формулы (3), полностью аналогично электростатики, получаем следующее уравнение Лапласа:

где ? – плотность массы. Это уравнение классической механики мы возьмем за основу и попробуем найти его релятивистский аналог.
При переходе к общей теории относительности мы должны заменить плотность массы ? релятивистски-инвариантной величиной. Такой величиной, причем примерно пропорциональным плотности ?, является тензор энергии-импульса T i j. Поскольку массы неподвижны, то потока энергии нет, и недиагональные элементы Тезора T i j равны нулю. Также мы можем пренебречь напряжениями внутри физического тела по сравнению с очень большой плотностью энергии покоя W = ? c 2. Таким образом, в нашем случае в тензора энергии-импульса отлична от нуля лишь одна временная компонента:

Этот тензор стоять (с некоторым коэффициентом пропорциональности) в правой части искомого уравнения – он порождает гравитацию. А что мы должны написать в левой части, т.е. такое гравитация? Ответ дал Эйнштейн, сформулировав принцип эквивалентности – это искривление четырехмерного пространства-времени. Сила тяжести вычисляется по той же формуле, что и силы инерции в неинерциальных системах координат:

Согласно ковариантная координата силы тяжести в трехмерном пространстве (знак минус учитывает псевдоевклидовисть):

В этой формуле производная координат берется по собственному времени ? материальной точки:

Мы возьмем для измерения силы тяжести недвижимое пробное тело массой m. Вдоль мировой линии этого тела зминюется только нулевая координата
 , Поэтому:
, Поэтому:
Приравнивая формулы (4) и (9) находим, что нулевая компонента метрического тензора связана с гравитационным потенциалом:

Константу интегрирования мы можем найти, зная что на бесконечности (вдали от тяготея тел) нулевая компонента метрического тензора равна единице, а потенциал превращается в ноль согласно формуле (3). Итак:

Теперь мы готовы подобрать релятивистский аналог для левой части формулы (5). Ясно, что этот аналог должен содержать вторую производную метрического тензора g i j и одновременно быть тензором, чтобы удовлетворить основное требование общей теории относительности – быть инвариантным относительно произвольной замены системы координат. Мы не можем использовать частные производные
 сами по себе, поскольку они не являются тензором (при замене системы координат преобразуются не по тензорным правилам. Также мы не можем воспользоваться ковариантной производной, поскольку известно, что ковариантная производная метрического тензора
сами по себе, поскольку они не являются тензором (при замене системы координат преобразуются не по тензорным правилам. Также мы не можем воспользоваться ковариантной производной, поскольку известно, что ковариантная производная метрического тензора  тождественно равна нулю. Но нам подходит тензор внутренней кривизны (тензор Римана):
тождественно равна нулю. Но нам подходит тензор внутренней кривизны (тензор Римана):

Ясно, что при малом искривлении пространства-времени мы можем выбрать близкую к декартовой системе координат. В ней символы Кристоффеля будут близки к нулю, так отбросив (два последних) квадратичные слагаемые в формуле (13) мы в правой части получим сумму вторых производных от метрического тензора. В этой сумме также будут приситни вторая производная от g 00, т.е. от гравитационного потенциала (формула 11).
Тензор кривизны R p i j k имеет четыре индекса, поэтому мы не можем его непосредственно приравнивать к тензора энергии-импульса T i j с двумя индексами. Уменьшить количество индексов можно, рассматривая линейные комбинации компонент тензора Римана (12). Очевидно, эти линейные комбинации тоже содержат сумму дугих производных от гравитационного потенциала ? (так что остается надежда получить аналог левой части формулы (5)). Мы не будем вводить новых физических величин, а воспользуемся для коэффициентов этих линейных комбинаций самым метрическим тензором – то есть рассмотрим свертки тензора Римана. Однократная свертка тензора
 по индексам (s j) дает тензор Риччи R_ {ik}:
по индексам (s j) дает тензор Риччи R_ {ik}:
Этот тензор симметричен и имеет два индекса, как и в тензора энергии-импульса T i j. Но кроме (14) мы можем образовать еще один симметричный тензор, умножив метрический тензор g i j на скалярную кривизну R, которая является сверткой тензора Риччи:

Итак естественными кандидатами на релятивистское обобщение уравнения (5) есть такие линейные комбинации:

где коэффициенты (?, ?, k) являются константами. Эти коэффициенты можно уточнить, воспользовавшись локальным законом сохранения энергии-импульса:

Итак дивергенция от левой части формулы (16) должна равняться нулю. Если бы тензор Римана был совсем произвольным, то добиться нулевой дивергенции мы не смогли бы ни при каких ненулевых константах (?, ?). Но к счастью, как чисто математическая свойство, ковариантные производные тензора Римана связанные дифференциальной тождеством Бианки:

Свернем эту тождественность сначала по индексам (k, q), а затем по (j, p):


Из последнего равенства, переименовав индекс, по которому проходит свертка, мы можем выразить дивергенцию тензора Риччи
 через градиент скалярной кривизны
через градиент скалярной кривизны  :
:
Теперь мы готовы, чтобы применить дивергенцию к уравнению (16):

Это равенство (закон сохранения энергии-импульса) будет тождественно выполняется, если коэффициент ? равен:

Ясно, что теперь коэффициент ? не может равняться нулю (иначе с учетом (23) и (16) тензор T i j был бы тождественным нулем). Делим равенство (16) на ? и перепозначимо пока неизвестную константу k. В результате приходим к такому уравнения гравитации:

Нам осталось найти константу k. Для этого надо показать, что в приближении слабого поля, левая часть уравнения (24) равна с некоторым коэффициентом лапласиана гравитационного потенциала
 и вычислить этот коэффициент. Это не совсем тривиально, поскольку кроме временной компоненты g 00 метрического тензора (формула 11), остальные компонент может также меняться. Детали вычисления смотрите в статье Слабое гравитационное поле.
и вычислить этот коэффициент. Это не совсем тривиально, поскольку кроме временной компоненты g 00 метрического тензора (формула 11), остальные компонент может также меняться. Детали вычисления смотрите в статье Слабое гравитационное поле.Выражение в левой части уравнения (24) является тензором Эйнштейна второй степени:

который можно получить вариацией интеграла Гаусса:

при изменении метрического тензора g i j на малую величину ? g i j. Кривизна Гаусса второй степерня K [2] равна половине скалярной кривизны:

Поскольку для материи (в частности для электромагнитного поля) тензор энергии-импульса тоже образуется из лагранжиана подобным образом как коэффициент при вариации метрики, например:

то отнимая от (28) предварительно умноженное уравнения (26) (с должным множителем, обратным к коэффициенту в правой части уравнения (1)) получим совокупный лагранжиан материи и гравитационного поля:

при вариации которого получается все: как уравнения Эйнштейна для гравитации, так и уравнения движения материи:

Второе слагаемое в правой части (29) является лагранжианом гравитационного поля:

Вариационный принцип встречается не только здесь, но во всех основных разделах физики: классической механике, квантовой механике, электродинамике, теории относительности. Такая распространенность наводит на мысль, что все законы физики связаны неким (еще неизвестным науке) одним универсальным уравнением. Это уравнение может образовываться вариацией "всеобщей действия" от некоторого общего лагранжиана. Сам Альберт Эйнштейн занимался поисками этого уравнения, хотя без значительных успехов. Одним из результатов Эйнштейна является поправка с космологической постоянной.
Рассмотрим вместо выражения (31) любую функцию от тензора Римана и его ковариантных производных, которая образует скаляр по тензорным правилам. Например:

Тогда при вариации этого обобщенного лагранжиана мы получим Обобщенный тензор Эйнштейна. Он подражает основные свойства тензора Эйнштейна (формула 25) второй степени: симметричный, релятивистски инвариантный, нулевая дивергенция. Единственное условие на поправки в формуле (32): они должны быть малыми в масштабах ближнего космоса (т.е. Солнечной системы), чтобы выполнялся закон тяготения Ньютона. Но в других масштабах они могут проявиться. В частности члены с
 при больших масштабах – вселенских и галактических. Квадратичные члены с
при больших масштабах – вселенских и галактических. Квадратичные члены с  могут проявиться в малых, в частности микроскопических масштабах. Подробнее это описано в статье Поправки к уравнению Эйнштейна.
могут проявиться в малых, в частности микроскопических масштабах. Подробнее это описано в статье Поправки к уравнению Эйнштейна.Уравнения Эйнштейна нелинейные и развязки можно найти в очень ограниченном количестве случаев. Известнейший развязок – метрика Шварцшильда для сферического распределения массы.
 Просмотров: 6357
Просмотров: 6357
 Дата: 20-02-2011
Дата: 20-02-2011
Теорема Нетер
Теорема Нетер – утверждение в теоретической физике, согласно которому каждой дифференцируемы симметрии соответствует интеграл движения. Например, однородности пространства соответствует закон
ПОДРОБНЕЕ
Тензор энергии-импульса
Тензор энергии-импульса – симметричный 4-тензор, определенный в пространстве-времени, который одновременно задает плотность энергии и ее потоков и определяет закон изменения этих величин при переходе
ПОДРОБНЕЕ
Метрика пространства-времени
Схематическое двумерных изображений искривления пространства-времени около массивного тела Метрика пространства-времени – 4-тензор, который определяет свойства пространства-времени в общей теории
ПОДРОБНЕЕ
Тензоры Эйнштейна и Риччи
Наряду с серией кривизн Гаусса m-й степени: естественно появляются (смотрите статью Интегралы Гаусса) следующие две серии тензоров второго ранга. Тензор Эйнштейна m-й степени: и тензоры Риччи m-й
ПОДРОБНЕЕ
Тензор кривизны
Тензор кривизны (Тензор внутренней кривизны многообразиях) появляется при рассмотрении коммутатора ковариантных производных ковариантного вектора (смотрите статью Дифференциальная геометрия) Вместо
ПОДРОБНЕЕ