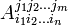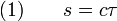Метрика пространства-времени

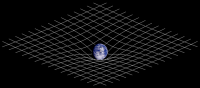Схематическое двумерных изображений искривления пространства-времени около массивного тела Метрика пространства-времени – 4-тензор, который определяет свойства пространства-времени в общей теории относительности.
Сказывается основном g i j.
В инерциальной системе отсчета матрица метрического тензора пространства-времени имеет вид

.

В неинерциальных системах отсчета вид метрики пространства-времени изменяется и вообще зависит от точки пространства и момента времени.
Метрика пространства-времени задает искривление пространства, которое ощущает наблюдатель, который движется с ускорением. Поскольку по принципу эквивалентности наблюдатель никаким образом не может отличить неинерцийнисть связанной с ним системы отсчета от гравитационного поля, то метрика пространства-времени определяет также искривление пространства в поле массивных тел.
Пространство-время выражается через метрику пространства-времени формуле

.

Поскольку метрика задает преобразование координат, то ее называют также метрическим тензором.
Метрика пространства-времени используется для установления связи между ковариантных и контравариантных записями любого 4-вектора

.

Метрический тензор симметричный относительно своих индексов, то есть g i j = g j i. Это видно из общей формулы для квадрата дифференциала пространственно-временного интрервалу. Детерминант метрики пространства времени, который обозначается g, отрицательный.
Контравариантный форма метрического тензора связана с ковариантной с помощью полностью антисимметричного тензора четвертого порядка

,

где e i j k l – обычный полностью антисимметричный тензор, определенный в инерционной системе отсчета, т.е. тензор, компоненты которого равны 1 или -1 и меняют знак при перестановке любых двух индексов.
Таким образом



Метрический тензор, как любой симметричный тензор, можно выбором системы отсчета свести к диагональному виду. Однако эта операция справедлива лишь в определенной точке пространства-времени, и, в общем случае, не может быть проведена для всего пространства-времени.
Квадрат дифференциала пространственно-временного интервала для одной пространственной точки равен

d s 2 = g 00 (d x 0) 2 = c 2 d ? 2,

где c – скорость света в вакууме.
Величину



называют собственным временем для данной точки пространства.
Квадрат расстояния между двумя бесконечно близкими точками задается формулой



Греческие индексы используются тогда, когда суммирование ведется только по пространственным координатам. Тензор ? ?? является метрическим тензором для трехмерного пространства.
Интегрировать определенную таким образом расстояние нельзя, так как результат зависел бы от мировой линии, по которой велось бы интегрирования. Таким образом, в общей теории относительности понятия расстояния между далекими объектами в трехмерном пространстве не имеет смысла. Единственное исключение – ситуация, в которой метрический тензор g i j не зависит от времени.