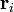Метрика Шварцшильда
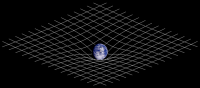
Метрика Шварцшильда – решение уравнений Эйнштейна для сферически-симметричного распределения масс в пустоте за пределами масс, описывающий искривленный пространство-время вокруг массивного тела. Это решение уравнений Эйнштейна получил в 1916 году Карл Шварцшильд. Его важность в том, что он теоретически определил возможность образования черных дыр.
В метрике Шварцшильда пространственно-временной интервал задается формулой.
 .
.
В этой формуле – Гравитационный радиус. Метрика зависит только от полной массы тел M. Другие величины в формуле: G – гравитационная постоянная, c – скорость света.
– Гравитационный радиус. Метрика зависит только от полной массы тел M. Другие величины в формуле: G – гравитационная постоянная, c – скорость света.
Метрика Шварцшильда справедлива не только для нерушимого тела, но и для тела, что может расширяться или сжиматься – необходимо только, чтобы оно оставалось сферически симметричным.
Для получения метрики внутри гравитационных масс необходимо знать распределение их плотности в пространстве или уравнения состояния.
Искривление пространства можно проиллюстрировать тем фактом, что расстояние между двумя точками r 1 и r 2 на одном луче равна

и больше r 2 – r 1. Это аналогично тому, как длина отрезка цепи между двумя точками на окружности больше длины хорды, соединяющей их.
Метрика Шварцшильда позволила определить искривления пути светового луча вблизи массивного тела, ставшего одним из экспериментальных подтверждений общей теории относительности.
Кроме того, анализ массивного тела показывает, что при достаточно большой массе, для такого тела может не отсутствовать стационарного радиуса, оно будет сжиматься. Процесс стистення получил название гравитационного коллапса.
В метрике Шварцшильда пространственно-временной интервал задается формулой.
 .
.В этой формуле
 – Гравитационный радиус. Метрика зависит только от полной массы тел M. Другие величины в формуле: G – гравитационная постоянная, c – скорость света.
– Гравитационный радиус. Метрика зависит только от полной массы тел M. Другие величины в формуле: G – гравитационная постоянная, c – скорость света.Метрика Шварцшильда справедлива не только для нерушимого тела, но и для тела, что может расширяться или сжиматься – необходимо только, чтобы оно оставалось сферически симметричным.
Для получения метрики внутри гравитационных масс необходимо знать распределение их плотности в пространстве или уравнения состояния.
Искривление пространства можно проиллюстрировать тем фактом, что расстояние между двумя точками r 1 и r 2 на одном луче равна

и больше r 2 – r 1. Это аналогично тому, как длина отрезка цепи между двумя точками на окружности больше длины хорды, соединяющей их.
Метрика Шварцшильда позволила определить искривления пути светового луча вблизи массивного тела, ставшего одним из экспериментальных подтверждений общей теории относительности.
Кроме того, анализ массивного тела показывает, что при достаточно большой массе, для такого тела может не отсутствовать стационарного радиуса, оно будет сжиматься. Процесс стистення получил название гравитационного коллапса.
 Просмотров: 2796
Просмотров: 2796
 Дата: 20-02-2011
Дата: 20-02-2011
Центр масс
Центр масс или центр масс системы материальных точек массой m i с радиус-векторами определяется как . В случае сплошного тела с плотностью Удобство введения понятия центра инерции в том, что
ПОДРОБНЕЕ
Уравнения Эйнштейна
Уравнения Эйнштейна – основные уравнения общей теории относительности. Неизвестной величиной в уравнениях Эйнштейна является метрический тензор g i k где R i k – тензор Риччи, R – скалярное
ПОДРОБНЕЕ
Метрика пространства-времени
Схематическое двумерных изображений искривления пространства-времени около массивного тела Метрика пространства-времени – 4-тензор, который определяет свойства пространства-времени в общей теории
ПОДРОБНЕЕ
Закон всемирного тяготения
Закон всемирного тяготения – физический закон, описывающий гравитационное взаимодействие в рамках ньютоновской механики. Закон утверждает, что сила притяжения между двумя телами (материальными
ПОДРОБНЕЕ
Черная дыра
Черные дыры – астрофизические объекты, которые создают настолько большую силу притяжения, что никакие частицы не могут оторваться на их поверхности. Поиски черных дыр во Вселенной – одна из
ПОДРОБНЕЕ
Пространство-время
Двумерная иллюстрация искривления пространства-времени вблизи массивного тела Пространство-время – искусственный математический 4-измеримое пространство событий. Положение любого события в
ПОДРОБНЕЕ