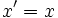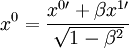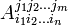Преобразования Лоренца
Преобразования Лоренца это линейные преобразования координат, оставляющие неизменным пространственно-временной интервал. Преобразования Лоренца связывают координаты событий в различных инерциальных системах отсчета и имеют фундаментальное значение в физике. Инвариантность физической теории относительно преобразований Лоренца, или релятивистская инвариантность, является необходимым условием достоверности этой теории.
Преобразования Лоренца в системах с параллельными осями
Наиболее распространенная форма записи преобразований Лоренца связывает координаты события в инерциальной системе отсчета K с координатами той же в события в системе K ', которая движется относительно K со скоростью V вдоль оси x:
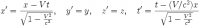 ,
,
где x, y, z, t – координаты события в системе K; x ', y', z ', t' – координаты того же события в системе K '; V – относительная скорость двух систем; c – скорость света.
Обратные формулы (переход от системы K 'в K) можно получить заменой V ->-V:
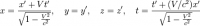 .
.
Матричный запись преобразований Лоренца
Часто, особенно в англоязычной литературе, преобразования Лоренца записываются в виде матрицы поворота | | ? ? '? | |, переводящий компоненты 4-вектора x ? системы K в компоненты 4-вектора x ?' = ? ? '? x ?, системы K ':
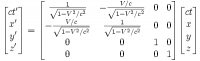 .
.
Формулы преобразований Лоренца с произвольной ориентацией осей систем
В случае когда оси x координатных систем не параллельные скорости формулы преобразования были получены Герглотцем в 1911 году. Для вывода этих формул удобно разделить радиус-вектор частицы r в системе K на компонента r | |, которая параллельна скорости V относительного движения инерциальных систем, и компонента r ?, перпендикулярной V. Тогда при переходе к другой системе K 'будет меняться только параллельная составляющая r | |:
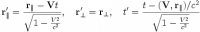
Окончательно радиус-вектор частицы в системе K 'r' = r '| | + r' ? формулы будут выглядеть так:
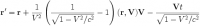 ,
,
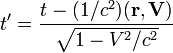 .
.
Гиперболическая форма записи
С математической точки зрения интервал между двумя событиями можно рассматривать как "расстояние" между двумя точками в четырехмерной системе координат. Итак, согласно определению, преобразование Лоренца должны сохранять неизменной любую длину в четырехмерном пространстве x, y, z, ct. Линейными преобразованиями с такими свойствами является лишь параллельные переносы и вращения системы координат. Параллельные переносы и вращения в плоскостях xy, yz, zx сводятся к переносу начала отсчета пространства и времени и обычным пространственным поворотам. Последние три поворота системы координат в плоскостях tx, ty, tz и есть преобразованиями Лоренца.
Если ввести "угол поворота" ?, такой что
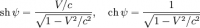 ,
,
то преобразования Лоренца для систем K и K 'с параллельными осями можно записать в гиперболической форме:
ct '= – x sh? + ct ch?,
x '= x ch? – ct sh?,
y '= y,
z '= z.
Эти формулы отличаются от обычных формул преобразования при поворотах системы координат заменой тригонометрических функций гиперболическими. В этом проявляются отмены псевдоевклидовои геометрии Минковского от обычной евклидовой.
Из формул преобразований легко увидеть, что при предельном переходе c -> ? к классической механики или – что то же самое – при скоростях значительно меньших скорости света формулы преобразования Лоренца переходят в преобразования Галилея по принципу соответствия.
При V> c координаты x, t становятся мнимыми, что означает тот факт, что движение со скоростью, превышающей скорость света в вакууме, невозможно. Невозможно также использовать систему отсчета, которая двигалась со скоростью света, потому что тогда знаменатели в формулах равнялись бы нулю.
В отличие от преобразований Галилея преобразования Лоренца некомутативни: результат двух последовательных преобразований Лоренца зависит от их порядка. Математически это можно увидеть с формальной толкование преобразований Лоренца как вращений четырехмерной системы координат, где, как известно, результат двух вращений вокруг различных осей зависит от порядка их выполнения. Исключением из этого правила являются лишь преобразования с параллельными векторами скоростей V 1 | | V 2, которые эквивалентны поворотам системы координат относительно одной оси.
Толчком к открытию преобразований Лоренца послужил нулевой результат интерференционного эксперимента Майкельсона-Морли. Для устранения выявленных проблем теории эфира Лоренц предположил, что все тела при постепенном движении изменяют свои размеры, а именно, что уменьшение размеров тела в направлении движения определяется множителем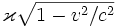 , Где
, Где 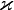 – Уменьшение размеров в направлении перпендикулярном движению тела. Необходимо было органично ввести это уменьшение размеров в теорию.
– Уменьшение размеров в направлении перпендикулярном движению тела. Необходимо было органично ввести это уменьшение размеров в теорию.
Первым формулы, известные сейчас как преобразование Лоренца, вывел Лармор в 1900 году, и таким образом учел изменения масштаба времени при движении. В 1904 Лоренц доказал инвариантность уравнений Максвелла относительно преобразований Лоренца, но у них еще входил неопределенный множитель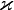 и две инерционные системы еще не рассматривались полностью равноправными.
и две инерционные системы еще не рассматривались полностью равноправными.
В 1905 Анри Пуанкаре исправил пробелы в работе Лоренца и достиг полной ковариантности электронной теории. Принцип относительности был определен им как общее и строгое положение. Именно в работах Пуанкаре впервые встречаются названия преобразования Лоренца и группа Лоренца.
Преобразования Лоренца в системах с параллельными осями
Наиболее распространенная форма записи преобразований Лоренца связывает координаты события в инерциальной системе отсчета K с координатами той же в события в системе K ', которая движется относительно K со скоростью V вдоль оси x:
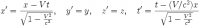 ,
,где x, y, z, t – координаты события в системе K; x ', y', z ', t' – координаты того же события в системе K '; V – относительная скорость двух систем; c – скорость света.
Обратные формулы (переход от системы K 'в K) можно получить заменой V ->-V:
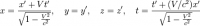 .
.Матричный запись преобразований Лоренца
Часто, особенно в англоязычной литературе, преобразования Лоренца записываются в виде матрицы поворота | | ? ? '? | |, переводящий компоненты 4-вектора x ? системы K в компоненты 4-вектора x ?' = ? ? '? x ?, системы K ':
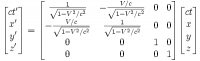 .
.Формулы преобразований Лоренца с произвольной ориентацией осей систем
В случае когда оси x координатных систем не параллельные скорости формулы преобразования были получены Герглотцем в 1911 году. Для вывода этих формул удобно разделить радиус-вектор частицы r в системе K на компонента r | |, которая параллельна скорости V относительного движения инерциальных систем, и компонента r ?, перпендикулярной V. Тогда при переходе к другой системе K 'будет меняться только параллельная составляющая r | |:
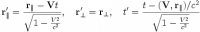
Окончательно радиус-вектор частицы в системе K 'r' = r '| | + r' ? формулы будут выглядеть так:
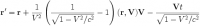 ,
,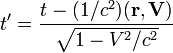 .
.Гиперболическая форма записи
С математической точки зрения интервал между двумя событиями можно рассматривать как "расстояние" между двумя точками в четырехмерной системе координат. Итак, согласно определению, преобразование Лоренца должны сохранять неизменной любую длину в четырехмерном пространстве x, y, z, ct. Линейными преобразованиями с такими свойствами является лишь параллельные переносы и вращения системы координат. Параллельные переносы и вращения в плоскостях xy, yz, zx сводятся к переносу начала отсчета пространства и времени и обычным пространственным поворотам. Последние три поворота системы координат в плоскостях tx, ty, tz и есть преобразованиями Лоренца.
Если ввести "угол поворота" ?, такой что
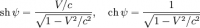 ,
,то преобразования Лоренца для систем K и K 'с параллельными осями можно записать в гиперболической форме:
ct '= – x sh? + ct ch?,
x '= x ch? – ct sh?,
y '= y,
z '= z.
Эти формулы отличаются от обычных формул преобразования при поворотах системы координат заменой тригонометрических функций гиперболическими. В этом проявляются отмены псевдоевклидовои геометрии Минковского от обычной евклидовой.
Из формул преобразований легко увидеть, что при предельном переходе c -> ? к классической механики или – что то же самое – при скоростях значительно меньших скорости света формулы преобразования Лоренца переходят в преобразования Галилея по принципу соответствия.
При V> c координаты x, t становятся мнимыми, что означает тот факт, что движение со скоростью, превышающей скорость света в вакууме, невозможно. Невозможно также использовать систему отсчета, которая двигалась со скоростью света, потому что тогда знаменатели в формулах равнялись бы нулю.
В отличие от преобразований Галилея преобразования Лоренца некомутативни: результат двух последовательных преобразований Лоренца зависит от их порядка. Математически это можно увидеть с формальной толкование преобразований Лоренца как вращений четырехмерной системы координат, где, как известно, результат двух вращений вокруг различных осей зависит от порядка их выполнения. Исключением из этого правила являются лишь преобразования с параллельными векторами скоростей V 1 | | V 2, которые эквивалентны поворотам системы координат относительно одной оси.
Толчком к открытию преобразований Лоренца послужил нулевой результат интерференционного эксперимента Майкельсона-Морли. Для устранения выявленных проблем теории эфира Лоренц предположил, что все тела при постепенном движении изменяют свои размеры, а именно, что уменьшение размеров тела в направлении движения определяется множителем
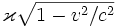 , Где
, Где 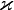 – Уменьшение размеров в направлении перпендикулярном движению тела. Необходимо было органично ввести это уменьшение размеров в теорию.
– Уменьшение размеров в направлении перпендикулярном движению тела. Необходимо было органично ввести это уменьшение размеров в теорию.Первым формулы, известные сейчас как преобразование Лоренца, вывел Лармор в 1900 году, и таким образом учел изменения масштаба времени при движении. В 1904 Лоренц доказал инвариантность уравнений Максвелла относительно преобразований Лоренца, но у них еще входил неопределенный множитель
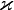 и две инерционные системы еще не рассматривались полностью равноправными.
и две инерционные системы еще не рассматривались полностью равноправными.В 1905 Анри Пуанкаре исправил пробелы в работе Лоренца и достиг полной ковариантности электронной теории. Принцип относительности был определен им как общее и строгое положение. Именно в работах Пуанкаре впервые встречаются названия преобразования Лоренца и группа Лоренца.
 Просмотров: 4693
Просмотров: 4693
 Дата: 19-02-2011
Дата: 19-02-2011
Преобразования Галилея
Преобразования Галилея – название преобразований в классической механике, согласно которым изменяются значения физических величин при переходе между различными инерционными системами отсчета.
ПОДРОБНЕЕ
4-вектор
4-вектор – это аналог трехмерного вектора в четырехмерном пространстве-времени, составленном переменными ct и x, y, z обычного пространства. В этом определении t – время, c – скорость света. При
ПОДРОБНЕЕ
4-тензор
4-тензор – математический объект, используемый для описания поля в релятивистской физике, тензор, определенный в четырехмерном пространстве-времени, повороты системы отсчета в котором включают как
ПОДРОБНЕЕ
Событие
Событие – изменение свойств объекта, взаимодействие между объектами, образование нового объекта или уничтожение существующего объекта. Каждое событие содержит оценку времени, указывает, когда оно
ПОДРОБНЕЕ
Инерционная система отсчета
Две системы отсчета, одна из которых движется со скоростью относительно другой Инерциальная система отсчета – система отсчета, в которой тело, на которое не действуют никакие силы, движется
ПОДРОБНЕЕ
Пространство-время
Двумерная иллюстрация искривления пространства-времени вблизи массивного тела Пространство-время – искусственный математический 4-измеримое пространство событий. Положение любого события в
ПОДРОБНЕЕ