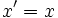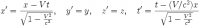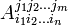4-вектор
4-вектор – это аналог трехмерного вектора в четырехмерном пространстве-времени, составленном переменными ct и x, y, z обычного пространства.
В этом определении t – время, c – скорость света.
При переходе от обычных векторов трехмерного пространства до 4-векторов основные уравнения физики набирают простой формы.
Каждое событие характеризуется местом и временем. То есть ее можно характеризовать с помощью четырех чисел: время t и декартовыми координатами x, y, z. Если домножить время на универсальную постоянную скорость света, то можно определить так называемый радиус-вектор в четырехмерном пространстве (x 0, x 1, x 2, x 3), где x 0 = c t, x 1 = x, x 2 = y, x 3 = z). Это пространство называют пространством Минковского.
Очевидно, что значение x, y, z зависят от выбора системы координат. При переходе от одной инерциальной системы координат к другой изменяется также значение времени згдино с преобразованиями Лоренца. Так при переходе к системе координат, которая движется относительно исходной системы со скоростью V вдоль оси x, получим:
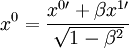
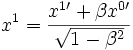 ,
,
где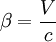 .
.
Радиус-вектор события является первым примером 4-вектора, который называют 4-радиус-вектором.
Произвольная четверка чисел (A 0, A 1, A 2, A 3), при переходе от одной системы координат в другую перетоврюеться аналогично 4-радиус-вектора называется ковариантрим 4-вектором.
Четверка чисел (A 0, – A 1 – A 2,-A 3) называется контравариантим 4-вектором. Контравариантный 4-векторы обозначаются нижними индексами.
(A 0, A 1, A 2, A 3) = (A 0, – A 1 – A 2,-A 3).
Скалярным произведением двух 4-векторов называется выражение
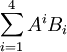 .
.
Знак суммы в скалярном произведении принято не писать, считая, что повторение индекса внизу и вверху автоматически означает суммирование по этому индексу.
Скалярное произведение 4-векторов при переходе к другой системе коодинат не меняется.
Иногда 4-векторы записываются в форме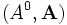 .
.
Четверка операторов
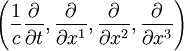
является контравариантный 4-Вектра, аналогом оператора градиента Гамильтона.
4-скорость визначается, как
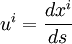
где ds – пространственно-временной интервал между бесконечно близкими событиями, и равна:
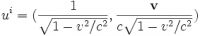 ,
,
где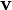 – Обычная трехмерная скорость. 4-скорость – безразмерная величина.
– Обычная трехмерная скорость. 4-скорость – безразмерная величина.
Для 4-скорости справедливо соотношение
u i u i = 1.
4-импульс частицы определяется, как
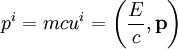 .
.
где m – масса частицы, E – энергия частицы.
Для 4-импульса справедливо соотношение: p i p i = m 2 c 2.
4-ускорение – это вторая производная от 4-радиуса относительно пространственно-временного интервала
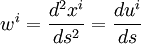 .
.
Для 4-ускорения справедливо соотношение
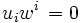 ,
,
есть 4-ускорения ортогональное до 4-скорости.
4-потенциал электромагнитного поля определяется как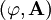 ,
,
где ? – электрический потенциал, а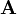 – Векторный потенциал магнитного поля.
– Векторный потенциал магнитного поля.
4-плотность тока определяется как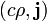 . Уравнение непрерывности тогда принимает форму Frac { partial j ^ i} { partial x ^ i} = 0 "src =" http://upload.wikimedia.org/math/9/7/1/971...c5c19ddbec7.png "/>, или в сокращенном виде
. Уравнение непрерывности тогда принимает форму Frac { partial j ^ i} { partial x ^ i} = 0 "src =" http://upload.wikimedia.org/math/9/7/1/971...c5c19ddbec7.png "/>, или в сокращенном виде 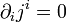 .
.
В этом определении t – время, c – скорость света.
При переходе от обычных векторов трехмерного пространства до 4-векторов основные уравнения физики набирают простой формы.
Каждое событие характеризуется местом и временем. То есть ее можно характеризовать с помощью четырех чисел: время t и декартовыми координатами x, y, z. Если домножить время на универсальную постоянную скорость света, то можно определить так называемый радиус-вектор в четырехмерном пространстве (x 0, x 1, x 2, x 3), где x 0 = c t, x 1 = x, x 2 = y, x 3 = z). Это пространство называют пространством Минковского.
Очевидно, что значение x, y, z зависят от выбора системы координат. При переходе от одной инерциальной системы координат к другой изменяется также значение времени згдино с преобразованиями Лоренца. Так при переходе к системе координат, которая движется относительно исходной системы со скоростью V вдоль оси x, получим:
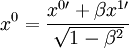
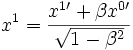 ,
,где
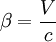 .
.Радиус-вектор события является первым примером 4-вектора, который называют 4-радиус-вектором.
Произвольная четверка чисел (A 0, A 1, A 2, A 3), при переходе от одной системы координат в другую перетоврюеться аналогично 4-радиус-вектора называется ковариантрим 4-вектором.
Четверка чисел (A 0, – A 1 – A 2,-A 3) называется контравариантим 4-вектором. Контравариантный 4-векторы обозначаются нижними индексами.
(A 0, A 1, A 2, A 3) = (A 0, – A 1 – A 2,-A 3).
Скалярным произведением двух 4-векторов называется выражение
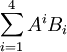 .
.Знак суммы в скалярном произведении принято не писать, считая, что повторение индекса внизу и вверху автоматически означает суммирование по этому индексу.
Скалярное произведение 4-векторов при переходе к другой системе коодинат не меняется.
Иногда 4-векторы записываются в форме
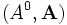 .
.Четверка операторов
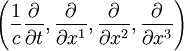
является контравариантный 4-Вектра, аналогом оператора градиента Гамильтона.
4-скорость визначается, как
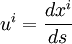
где ds – пространственно-временной интервал между бесконечно близкими событиями, и равна:
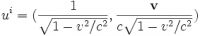 ,
,где
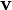 – Обычная трехмерная скорость. 4-скорость – безразмерная величина.
– Обычная трехмерная скорость. 4-скорость – безразмерная величина.Для 4-скорости справедливо соотношение
u i u i = 1.
4-импульс частицы определяется, как
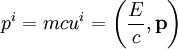 .
.где m – масса частицы, E – энергия частицы.
Для 4-импульса справедливо соотношение: p i p i = m 2 c 2.
4-ускорение – это вторая производная от 4-радиуса относительно пространственно-временного интервала
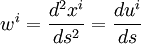 .
.Для 4-ускорения справедливо соотношение
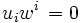 ,
,есть 4-ускорения ортогональное до 4-скорости.
4-потенциал электромагнитного поля определяется как
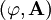 ,
,где ? – электрический потенциал, а
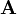 – Векторный потенциал магнитного поля.
– Векторный потенциал магнитного поля.4-плотность тока определяется как
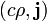 . Уравнение непрерывности тогда принимает форму Frac { partial j ^ i} { partial x ^ i} = 0 "src =" http://upload.wikimedia.org/math/9/7/1/971...c5c19ddbec7.png "/>, или в сокращенном виде
. Уравнение непрерывности тогда принимает форму Frac { partial j ^ i} { partial x ^ i} = 0 "src =" http://upload.wikimedia.org/math/9/7/1/971...c5c19ddbec7.png "/>, или в сокращенном виде 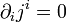 .
. Просмотров: 2967
Просмотров: 2967
 Дата: 19-02-2011
Дата: 19-02-2011
Динамическая система
Фазовая диаграмма аттрактора Лоренца – популярный пример нелинейного динамически системы. Подобные системы изучает теория хаоса Динамическая система – математическая абстракция, предназначенная для
ПОДРОБНЕЕ
Вектор состояния
Вектор состояния – совокупность характеристик, однозначно определяют состояние квантовой системы. Понятие вектор состояния является обобщением понятия волновой функции. Волновая функция, эволюция
ПОДРОБНЕЕ
Преобразования Галилея
Преобразования Галилея – название преобразований в классической механике, согласно которым изменяются значения физических величин при переходе между различными инерционными системами отсчета.
ПОДРОБНЕЕ
Преобразования Лоренца
Преобразования Лоренца это линейные преобразования координат, оставляющие неизменным пространственно-временной интервал. Преобразования Лоренца связывают координаты событий в различных инерциальных
ПОДРОБНЕЕ
4-тензор
4-тензор – математический объект, используемый для описания поля в релятивистской физике, тензор, определенный в четырехмерном пространстве-времени, повороты системы отсчета в котором включают как
ПОДРОБНЕЕ
Пространство-время
Двумерная иллюстрация искривления пространства-времени вблизи массивного тела Пространство-время – искусственный математический 4-измеримое пространство событий. Положение любого события в
ПОДРОБНЕЕ