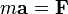Момент инерции
Момент инерции (единица измерения в системе [кг м 2]) – в физике является мерой инерции вращательного движения, аналогично массе для поступательного.
В общем случае, значение момента инерции объекта зависит от его формы и распределения массы в объеме: чем больше массы сконцентрировано дальше от центра масс тела, тем больше его момент инерции. Также его значение зависит от выбранной оси вращения.
Твердое тело можно рассматривать как систему из бесконечного количества материальных точек, каждая с массой m i. Если расстояния от каждой точки до оси вращения равны r i, то момент инерции тела к выбранной оси определяется как:
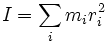
В условиях непрерывного распределения массы в теле, нужен переход к интегральной формы закона:
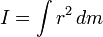
где элемент массы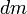 определяется с помощью пространственного распределения плотности
определяется с помощью пространственного распределения плотности 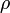 .
.
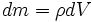
В общем случае вращения твердого тела произвольной формы сложнее. Тело характеризуется тензором второго ранга
где индексы ? и ? пробегают значения координат x, y, z.
Тензор инерции симметричный
I ?? = I ??.
Как и для любого другого тенозру второго ранга, его можно упростить, перейдя к системе координат, в которой он имеет диагональную форму (главной системы координат). Оси главной системы координат называют главными осями инерции.
Момент инерции твердого тела относительно произвольной оси зависит не только от массы, формы и размеров тела, но также от положения тела относительно этой оси. Согласно теореме Штейнера (теоремой Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J c относительно оси, проходящей через центр массы тела параллельно оси, рассматривается, и произведения массы тела m на квадрат расстояния d между осями между осями:
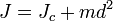
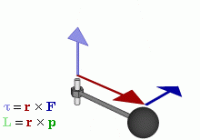
Момент импульса тела при вращении зависит от вектора угловой скорости и тензора инерциии
В главной системе координат
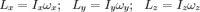 .
.
Кинетическая энергия вращения тела задается формулой
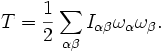
В главной системе координат
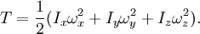
По аналогии со вторым законом Ньютона для поступательного движения, можно сформулировать уравнения вращательного движения, где внешним силам, которые действуют на тело, отвечают моменты сил, массе – момент инерции, а ускорению – угловое ускорение.
При одноосном вращении
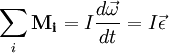
Здесь M i – моменты внешних сил,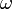 – Угловая скорость,
– Угловая скорость,  – Угловое ускорение.
– Угловое ускорение.
В общем случае, значение момента инерции объекта зависит от его формы и распределения массы в объеме: чем больше массы сконцентрировано дальше от центра масс тела, тем больше его момент инерции. Также его значение зависит от выбранной оси вращения.
Твердое тело можно рассматривать как систему из бесконечного количества материальных точек, каждая с массой m i. Если расстояния от каждой точки до оси вращения равны r i, то момент инерции тела к выбранной оси определяется как:
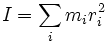
В условиях непрерывного распределения массы в теле, нужен переход к интегральной формы закона:
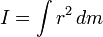
где элемент массы
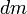 определяется с помощью пространственного распределения плотности
определяется с помощью пространственного распределения плотности 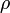 .
.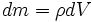
В общем случае вращения твердого тела произвольной формы сложнее. Тело характеризуется тензором второго ранга
где индексы ? и ? пробегают значения координат x, y, z.
Тензор инерции симметричный
I ?? = I ??.
Как и для любого другого тенозру второго ранга, его можно упростить, перейдя к системе координат, в которой он имеет диагональную форму (главной системы координат). Оси главной системы координат называют главными осями инерции.
Момент инерции твердого тела относительно произвольной оси зависит не только от массы, формы и размеров тела, но также от положения тела относительно этой оси. Согласно теореме Штейнера (теоремой Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J c относительно оси, проходящей через центр массы тела параллельно оси, рассматривается, и произведения массы тела m на квадрат расстояния d между осями между осями:
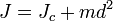
Момент импульса тела при вращении зависит от вектора угловой скорости и тензора инерциии
В главной системе координат
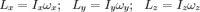 .
.Кинетическая энергия вращения тела задается формулой
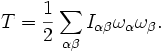
В главной системе координат
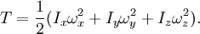
По аналогии со вторым законом Ньютона для поступательного движения, можно сформулировать уравнения вращательного движения, где внешним силам, которые действуют на тело, отвечают моменты сил, массе – момент инерции, а ускорению – угловое ускорение.
При одноосном вращении
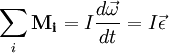
Здесь M i – моменты внешних сил,
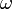 – Угловая скорость,
– Угловая скорость,  – Угловое ускорение.
– Угловое ускорение. Просмотров: 3953
Просмотров: 3953
 Дата: 24-02-2011
Дата: 24-02-2011
Инерция
Инерция – свойство тела сохранять равномерное прямолинейное движение или покой, что внешняя причина (сила, или действие другого тела) не выведет его из этого состояния. Мерой инерции тела
ПОДРОБНЕЕ
Центр масс
Центр масс или центр масс системы материальных точек массой m i с радиус-векторами определяется как . В случае сплошного тела с плотностью Удобство введения понятия центра инерции в том, что
ПОДРОБНЕЕ
Сила Кориолиса
Сила Кориолиса (по имени французского ученого Г. Г. Кориолиса) – одна из сил инерции, существующая в системе отсчета, вращающейся и проявляется при движении в направлении под углом к оси вращения.
ПОДРОБНЕЕ
Момент импульса
Моментом импульса называется векторная величина, характеризующая инерционные свойства объекта, осуществляющего вращательное движение относительно определенной точки (начала координат). Определение
ПОДРОБНЕЕ
Масса
Масса – физическая величина, являющаяся одной из основных характеристик материи, определяющая ее инерционные, энергетические и гравитационные свойства. Масса обычно обозначается латинской буквой
ПОДРОБНЕЕ
Принцип эквивалентности
Принцип эквивалентности – основное утверждение общей теории относительности, по которому наблюдатель не может никоим образом отличить действие гравитационного поля от силы инерции, возникающая в
ПОДРОБНЕЕ