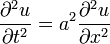Математическая модель
Математическая модель (рус. математическая модель, англ. Mathematic model; нем. Mathematisches Model n) – система математических соотношений, описывающих исследуемый процесс или явление. Математическая модель имеет важное значение для таких наук, как: экономика, экология, социология, физика, химия, механика, информатика, биология и др.
При получении г.г. используют общие законы естествознания, специальные законы конкретных наук, результаты пассивных и активных экспериментов, имитационное моделирование с помощью ЭВМ. Г.г. позволяют предвидеть ход процесса, рассчитать целевую функцию (выходные параметры процесса), управлять процессом, проектировать системы с желаемыми характеристиками.
Для создания математических моделей можно использовать любые математические средства – язык дифференциальных или интегральных уравнений, теории множеств, абстрактной алгебры, математической логике, теории вероятностей, графы и другие. Процесс создания математической модели называется математическим моделированием. Это самый общий и наиболее используемый в науке, в частности, в кибернетике, метод исследований.
Если отношение задаются аналитически, то их можно решить в замкнутом виде (явно) относительно искомых переменных как функции от параметров модели, либо в частично замкнутом виде (неявно), когда искомые переменные зависят от одного или многих параметров модели. К моделям этого класса относятся дифференциальные, интегральные, разностные уравнения, вероятностные модели, модели математического программирования и другие.
Если нельзя получить точное решение математической модели, используются численные (вычислительные) методы или другие виды моделирования.
В зависимости от того, каковы параметры системы и внешние возмущения г.г. могут быть детерминированными и стохастическими. Последние имеют особенно важное значение при исследовании и проектировании больших систем со сложными связями и свойствами, которые трудно учесть. Математическое описание непрерывного процесса (напр., дифференциальными уравнениями) представляет собой непрерывную г.г.
Если же г.г. описывает состояние системы только для дискретных значений независимой переменной и пренебрегает характером процессов, протекающих в промежутках между ними, то такая модель является дискретной (здесь важен выбор шага дискретности, от которого зависит точность описания реального объекта его М.М.). Если параметры объекта, для которого разрабатывают М.М., можно считать независимыми от времени, то такая система описывается стационарной моделью, характерная особенность которой – постоянные коэффициенты. В противном случае Н.Н. является нестационарной.
При математическом моделировании ориентируются на модели стандартного вида, которые обеспечены соответствующим математическим аппаратом. Так физические процессы характеризуются пространственно-временными соотношениями и в общем случае описываются дифференциальными уравнениями в частных производных.
Важным моментом структурирования модели является феноменологический метод, когда субпроцессов могут быть представлены отдельными моделями, выходные величины которых являются входными для других (последующих) субпроцессов. В этом случае Н.Н. сложного процесса представляет собой систему моделей (уравнений), найденных для каждого субпроцессов.
Для разработки г.г. широко используется дифференциальное исчисление, теория множеств, матрицы и графы, а также планирования эксперимента. Соответственно различают теоретико-множественные, матричные, топологические и полиномни г.г. Примеры моделей:
При получении г.г. используют общие законы естествознания, специальные законы конкретных наук, результаты пассивных и активных экспериментов, имитационное моделирование с помощью ЭВМ. Г.г. позволяют предвидеть ход процесса, рассчитать целевую функцию (выходные параметры процесса), управлять процессом, проектировать системы с желаемыми характеристиками.
Для создания математических моделей можно использовать любые математические средства – язык дифференциальных или интегральных уравнений, теории множеств, абстрактной алгебры, математической логике, теории вероятностей, графы и другие. Процесс создания математической модели называется математическим моделированием. Это самый общий и наиболее используемый в науке, в частности, в кибернетике, метод исследований.
Если отношение задаются аналитически, то их можно решить в замкнутом виде (явно) относительно искомых переменных как функции от параметров модели, либо в частично замкнутом виде (неявно), когда искомые переменные зависят от одного или многих параметров модели. К моделям этого класса относятся дифференциальные, интегральные, разностные уравнения, вероятностные модели, модели математического программирования и другие.
Если нельзя получить точное решение математической модели, используются численные (вычислительные) методы или другие виды моделирования.
В зависимости от того, каковы параметры системы и внешние возмущения г.г. могут быть детерминированными и стохастическими. Последние имеют особенно важное значение при исследовании и проектировании больших систем со сложными связями и свойствами, которые трудно учесть. Математическое описание непрерывного процесса (напр., дифференциальными уравнениями) представляет собой непрерывную г.г.
Если же г.г. описывает состояние системы только для дискретных значений независимой переменной и пренебрегает характером процессов, протекающих в промежутках между ними, то такая модель является дискретной (здесь важен выбор шага дискретности, от которого зависит точность описания реального объекта его М.М.). Если параметры объекта, для которого разрабатывают М.М., можно считать независимыми от времени, то такая система описывается стационарной моделью, характерная особенность которой – постоянные коэффициенты. В противном случае Н.Н. является нестационарной.
При математическом моделировании ориентируются на модели стандартного вида, которые обеспечены соответствующим математическим аппаратом. Так физические процессы характеризуются пространственно-временными соотношениями и в общем случае описываются дифференциальными уравнениями в частных производных.
Важным моментом структурирования модели является феноменологический метод, когда субпроцессов могут быть представлены отдельными моделями, выходные величины которых являются входными для других (последующих) субпроцессов. В этом случае Н.Н. сложного процесса представляет собой систему моделей (уравнений), найденных для каждого субпроцессов.
Для разработки г.г. широко используется дифференциальное исчисление, теория множеств, матрицы и графы, а также планирования эксперимента. Соответственно различают теоретико-множественные, матричные, топологические и полиномни г.г. Примеры моделей:
 Просмотров: 3078
Просмотров: 3078
 Дата: 27-03-2011
Дата: 27-03-2011
Математическая логика
Математическая логика является наукой о законах математического мышления. Предметом математической логики есть математические теории в целом, которые изучаются с помощью логико-математических языков.
ПОДРОБНЕЕ
Математическая статистика
Математическая статистика – раздел математики, в котором на основе опытных данных изучаются вероятностные закономерности массовых явлений. Основными задачами математической статистики является
ПОДРОБНЕЕ
Математическая основа карт
Математическая основа карт (рус. математическая основа карт, англ. Mathematical base of maps, нем. Mathematische Grundlage f der Karten) – совокупность элементов, обуславливающих математические
ПОДРОБНЕЕ
Модель (общее значение)
Пример научного моделирования. Схема химических процессов и процессов переноса в атмосфере. Модель машины скорой помощи Модель (рус. модель, англ. Model, нем. Modell n, фр. Modele, от лат. Modulus –
ПОДРОБНЕЕ
Математическая физика
Математическая физика – общее название математических методов исследования и решения дифференциальных уравнений физики. Теория математических моделей физических явлений; занимает особое положение и в
ПОДРОБНЕЕ
Математическая биология
Математическая биология (также известная как математическое биомоделювання или биоматематика) - междисциплинарная область академических исследований, часто рассматривается как подразделение
ПОДРОБНЕЕ