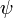Дельта-функция
?-функция – это обобщенная функция, формально определяется как непрерывный линейный функционал в пространстве дифференцируемых функций. ?-функция не является функцией в классическом понимании.
Введена английским физиком Дираком. Позволяет записать пространственную плотность физической величины (масса, заряд, интенсивность источника тепла, сила и т. п.), сосредоточенной или приложенной в одной точке. Например, плотность точечной массы m, находящейся в точке a евклидова пространства , Записывается с помощью ?-функции в виде
, Записывается с помощью ?-функции в виде  .
.
?-функция определяется формальным соотношением

для любой непрерывной функции .
.
Для дельта-функции одной переменной верны следующие равенства:
Во многих случаях удобным оказывается такое представление дельта-функции:
Рассмотрим интеграл
 , (1)
, (1)
который можно интерпретировать как предел
 . (2)
. (2)
Известно, что
 . (3)
. (3)
В силу (3) для любого справедливо равенство:
справедливо равенство:
 . (4)
. (4)
Можно показать, что при неограниченном росте оказываются верными все свойства дельта-функции и функции (2) направляется в
оказываются верными все свойства дельта-функции и функции (2) направляется в  ; Это позволяет сделать вывод, что:
; Это позволяет сделать вывод, что:
 .
.
Фундаментальный выражение, описывающий производную дельта-функции ? (x):
 .
.
Подставив , Получим выражение:
, Получим выражение:
 .
.
После преобразования имеем:
 .
.
Поскольку , Получаем окончательное выражение
, Получаем окончательное выражение
 .
.
В общем виде выражение производной дельта-функции записывается так:
 .
.
Для производной дельта-функции верны следующие тождества:
 ;
;
 ;
;
 .
.
До начала координат x (t) = ? (t) можно применить преобразование Фурье:

в результате получается, что спектр ?-функции является константой: F (?) = 1.
Доказано, что производная функции Хевисайда равна дельта-функции. Т.е. функция показано выше функции:
 .
.
Следовательно, применив преобразование Фурье к дельта-функции
 ,
,
получим ее образ в виде:
 .
.
В двумерном пространстве:
 ;
;
 .
.
В полярных координатах:
 .
.
В трехмерном пространстве:
 ;
;
 .
.
В цилиндрической системе:
 .
.
В сферической системе координат:
 .
.
 График функции Хевисайда, производная от которой – дельта-функция
График функции Хевисайда, производная от которой – дельта-функция  Дельта-функция
Дельта-функция
Мгновенное ускорение
Примером применения дельта-функции Дирака может служить задача о столкновении двух тел. Если на ударе налетает другое, то оба тела получают ускорение и скорость. Как рассчитать ускорение, приобретенное телом? Построим график скорости от времени. График будет иметь вид, показанный на верхнем рисунке справа. На нижнем рисунке приведен график дельта-функции с единичной амплитудой, он отражает мгновенный процесс набора скорости телом.
Принимая во внимание то, что модель рассматривается в евклидовом пространстве, можно записать следующее уравнение:
a (t) = ?? (t – t a).
Функция Грина
Другие примеры Дельта-функция применяется в математической физике при решении задач, в которые входят сосредоточенные величины. В квазиклассическом волновые функции локализуются в дельта-функции, а центры их сосредоточения движутся по классическим траекториям по уравнениям Ньютона. Через дельта-функцию, также записуется функция Грина линейного оператора L, действующего на обобщенные функции над многообразием M в точке x 0. Уравнение имеет вид
волновые функции локализуются в дельта-функции, а центры их сосредоточения движутся по классическим траекториям по уравнениям Ньютона. Через дельта-функцию, также записуется функция Грина линейного оператора L, действующего на обобщенные функции над многообразием M в точке x 0. Уравнение имеет вид  .
.
где – Оператор Лапласа.
– Оператор Лапласа.
Важно отметить следующую формулу
 ,
,
где
 – Функция Грина.
– Функция Грина.
Это выражение следует из того, что ведет себя подобно дельта-функции.. Этот факт используется для доказательства того, что выражение для скалярного потенциала:
ведет себя подобно дельта-функции.. Этот факт используется для доказательства того, что выражение для скалярного потенциала:

удовлетворяет уравнению Пуассона:
 .
.
Таким образом, дельта-функция является мощным математическим аппаратом для описания сложных физических процессов.
Введена английским физиком Дираком. Позволяет записать пространственную плотность физической величины (масса, заряд, интенсивность источника тепла, сила и т. п.), сосредоточенной или приложенной в одной точке. Например, плотность точечной массы m, находящейся в точке a евклидова пространства
 , Записывается с помощью ?-функции в виде
, Записывается с помощью ?-функции в виде  .
.?-функция определяется формальным соотношением

для любой непрерывной функции
 .
.Для дельта-функции одной переменной верны следующие равенства:
Во многих случаях удобным оказывается такое представление дельта-функции:
Рассмотрим интеграл
 , (1)
, (1)который можно интерпретировать как предел
 . (2)
. (2)Известно, что
 . (3)
. (3)В силу (3) для любого
 справедливо равенство:
справедливо равенство: . (4)
. (4)Можно показать, что при неограниченном росте
 оказываются верными все свойства дельта-функции и функции (2) направляется в
оказываются верными все свойства дельта-функции и функции (2) направляется в  ; Это позволяет сделать вывод, что:
; Это позволяет сделать вывод, что: .
.Фундаментальный выражение, описывающий производную дельта-функции ? (x):
 .
.Подставив
 , Получим выражение:
, Получим выражение: .
.После преобразования имеем:
 .
.Поскольку
 , Получаем окончательное выражение
, Получаем окончательное выражение .
.В общем виде выражение производной дельта-функции записывается так:
 .
.Для производной дельта-функции верны следующие тождества:
 ;
; ;
; .
.До начала координат x (t) = ? (t) можно применить преобразование Фурье:

в результате получается, что спектр ?-функции является константой: F (?) = 1.
Доказано, что производная функции Хевисайда равна дельта-функции. Т.е. функция показано выше функции:
 .
.Следовательно, применив преобразование Фурье к дельта-функции
 ,
,получим ее образ в виде:
 .
.В двумерном пространстве:
 ;
; .
.В полярных координатах:
 .
.В трехмерном пространстве:
 ;
; .
.В цилиндрической системе:
 .
.В сферической системе координат:
 .
. График функции Хевисайда, производная от которой – дельта-функция
График функции Хевисайда, производная от которой – дельта-функция  Дельта-функция
Дельта-функцияМгновенное ускорение
Примером применения дельта-функции Дирака может служить задача о столкновении двух тел. Если на ударе налетает другое, то оба тела получают ускорение и скорость. Как рассчитать ускорение, приобретенное телом? Построим график скорости от времени. График будет иметь вид, показанный на верхнем рисунке справа. На нижнем рисунке приведен график дельта-функции с единичной амплитудой, он отражает мгновенный процесс набора скорости телом.
Принимая во внимание то, что модель рассматривается в евклидовом пространстве, можно записать следующее уравнение:
a (t) = ?? (t – t a).
Функция Грина
Другие примеры Дельта-функция применяется в математической физике при решении задач, в которые входят сосредоточенные величины. В квазиклассическом
 волновые функции локализуются в дельта-функции, а центры их сосредоточения движутся по классическим траекториям по уравнениям Ньютона. Через дельта-функцию, также записуется функция Грина линейного оператора L, действующего на обобщенные функции над многообразием M в точке x 0. Уравнение имеет вид
волновые функции локализуются в дельта-функции, а центры их сосредоточения движутся по классическим траекториям по уравнениям Ньютона. Через дельта-функцию, также записуется функция Грина линейного оператора L, действующего на обобщенные функции над многообразием M в точке x 0. Уравнение имеет вид  .
.где
 – Оператор Лапласа.
– Оператор Лапласа.Важно отметить следующую формулу
 ,
,где
 – Функция Грина.
– Функция Грина.Это выражение следует из того, что
 ведет себя подобно дельта-функции.. Этот факт используется для доказательства того, что выражение для скалярного потенциала:
ведет себя подобно дельта-функции.. Этот факт используется для доказательства того, что выражение для скалярного потенциала:
удовлетворяет уравнению Пуассона:
 .
.Таким образом, дельта-функция является мощным математическим аппаратом для описания сложных физических процессов.
 Просмотров: 5239
Просмотров: 5239
 Дата: 19-02-2011
Дата: 19-02-2011
Вариационное исчисление
Вариационное исчисление – это раздел функционального анализа, который занимается дифференцированием функционалов. Примечание: функционалы можно интегрировать по пространству функций. Эту операцию
ПОДРОБНЕЕ
Собственная функция
Собственной функцией линейного оператора L с собственным значением ? называется такая ненулевая функция f, для которой выполняется соотношение L (f) = ? f, где ? это определенное число
ПОДРОБНЕЕ
Амплитуда вероятности
Амплитуда вероятности – комплексная величина, квадрат модуля которой задает плотность вероятности. В частности, в квантовой механике волновая функция ? является амлитудою вероятности нахождения
ПОДРОБНЕЕ
Функция распределения вероятностей
Функция распределения вероятностей – В теории вероятностей это функция, которая полностью описывает распределение вероятностей случайной величины. Пусть – Вероятностное пространство, в котором ? –
ПОДРОБНЕЕ
Корреляционная функция
Корреляционная функция – функция времени или пространственных координат, которая задает корреляцию в системах со случайными процессами. Зависящая от времени корреляция двух случайных функций X (t) и
ПОДРОБНЕЕ
Волновая функция
Волновая функция, или пси-функция – Основной математический объект квантовой механики при ее формулировке, как волновой механики. В простейшем случае это комплексная квадратично интегрируема функция
ПОДРОБНЕЕ