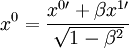Собственный вектор

На изображении мы видим транформации сдвига, что происходит с Джокондой. Синий вектор меняет направление, а красный – нет. Поэтому красный является собственным вектором такого преобразования, а синий – нет. Так как красный вектор ни растянулся, ни сжался, его собственное значение равно единице. Все векторы коллинеарны красном тоже собственные Собственный вектор (англ. eigenvector) квадратной матрицы (С собственным значением (англ. eigenvalue) ) – Это ненулевой вектор , Для которого выполняется соотношение



где ? это определенный скаляр, то есть действительное или комплексное число.
То есть, собственные векторы матрицы A – это ненулевые векторы, которые под действием линейного преобразования задаваемый матрицей A не меняют направления, но могут изменять длину на коэффициент ?.
Матрица размерами имеет не более N собственных векторов и собственных значений, соответствующих им.
Соотношение (*) имеет смысл также для линейного оператора в векторном пространстве V. Если это пространство – конечномерных, то оператор можно записать в виде матрицы относительно определенно базиса V.
Поскольку собственные векторы и собственные значения было обозначено без применения координат, не зависящие от выбора базиса. Поэтому подобные матрицы имеют одинаковые собственные значения.
Ведущую роль в понимании собственных значений матриц играет теорема Гамильтона-Кэли. Из нее следует, что собственные значения матрицы A и только они являются корнями характеристического полинома матрицы A:



p (?) является полиномом степени n, следовательно по основной теореме алгебры, существует ровно n комплексных собственных значений, учитывая их кратности.
Итак, матрица A имеет не более n собственных значений (но множество собственных векторов для каждого из них).
Запишем характеристический полином через его корни:



Кратность корня характеристического полинома матрицы называется алгебраической кратностью собственного значения
Совокупность всех собственных значений матрицы или линейного оператора в конечномерных векторном пространстве называется спектром матрицы или линейного оператора. (Эта терминология видоизменяется для нескинченозмирних векторных пространств: в общем случае, к спектру оператора могут принадлежать ?, которые не являются собственными значениями.)
Благодаря связи характеристического полинома матрицы с ее собственными значениями, последние еще называют характеристическим числами матрицы.
Для каждого собственного значения , Получим свою систему уравнений:



что будет иметь линейно независимых решений.
Совокупность всех решений системы образует линейный подпространство размерности и называется собственным пространством (англ. eigenspace) матрицы с собственным значением .
Размерность собственного пространства называется геометрической кратностью соответствующего собственного значения ?.
Все собственные пространства являются инвариантными подпространствами для .
Если существуют не менее двух линейно-независимые собственные векторы с одинаковым собственным значением ?, то такое собственное значение называется вырожденным. Эта терминология используется преимущественно в том случае, если геометрическая и алгебраическая кратности собственных значений совпадают, например, для эрмитовых матриц.






где – Квадратная матрица размера n x n, -Тый столбец которой является вектор , А – Это диагональная матрица с соответствующими значениями .



Проблемой собственных значений называется задача нахождения собственных векторов и чисел матрицы.
По определению (с помощью характеристического уравнения) можно находить только собственные значения матриц размерности менее пяти. Характеристическое уравнение имеет степень равную степени матрицы. Для больших степеней нахождения решений уравнения становится очень проблематичным, поэтому используют различные численные методы
Разные задачи требуют получения разного количества собственных значений. Поэтому различают несколько проблем поиска собственных значений, для каждой из которых используют свои методы.
Казалось бы частичная проблема собственных значений является частичной проблемой полной, и решается теми же методами что и полная. Однако, методы применяемые к частных задач гораздо эффективнее, поэтому могут применяться к матриц большой размерности (например в ядерной физике возникают проблемы нахождения собственных значений для матриц размерности 10 3 – 10 6).
Метод Якоби



Одним из старейших и наиболее общих подходов к решению полной проблемы собственных значений является метод Якоби, впервые был опубликован в 1846.
Метод применяют к симметричной матрицы A
Это простой итеративный алгоритм, в котором матрица с собственными векторами вычисляется последовательностью умножений.